Soluzione all'enigma 66, proposto da Paolo C. il 13 marzo 2006

È possibile (e se si dire come, magari con un disegnino) disporre 5 monete in modo che ugnuna di esse sia a contatto con tutte le altre?
Si considerino le monete rotonde e tutte uguali. [Per i più pignoli: la soluzione che ho in mente funziona sia nel caso ideale di 5 circonferenze, ma anche nel caso di cilindri a patto che l'altezza del cilindro sia piccola rispetto al diametro... adesso non saprei quantificare, ma direi che l'altezza dovrebbe essere meno di un decimo del diametro, o giù di lì... più o meno come nel caso delle monete reali. Direi che le monete da 1 euro possono essere un buon modello per provare... Il fatto che le monete reali abbiano gli spigoli un po'
arrotondati è influente.]

Ecco la soluzione di Anita:

Metto la prima moneta orizzontalmente sul piano e altre due le dispongono orizzontalmente sopra la prima congiungendosi nel centro di essa (perciò queste si toccano tutte e 3). Le ultime 2 monete le metto diagonalmente in modo che si tocchino a spiovente (^) toccando entrambe anche le altre 3 monete. Praticamente le ultime 2 monete partono dagli estremi della prima moneta e ,chiudendosi a spiovente, toccano le 2 monete che si appoggiano sulla prima. Quindi le monete sono tutte a contatto.

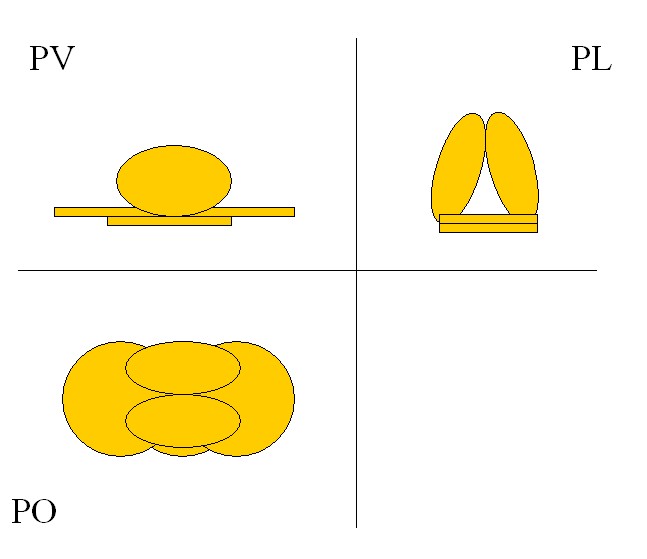
Ed ecco l'immagine preparata da Paolo per descrivere tale situazione

: