Quanti sono i poliedri regolari (convessi)?

I poliedri regolari sono quei poliedri che hanno tutte le facce uguali tra loro, costituite da poligoni regolari, e tutti gli angoli solidi (o angoloidi) uguali tra loro. I poliedri regolari convessi sono anche detti solidi platonici. Osservando e maneggiando i poliedri da noi costruiti, esscludiamo tutti quelli le cui facce non sono poligoni regolari, escludiamo quelli le cui facce non sono tutte uguali ed escludiamo quelli i cui angoli solidi non sono tutti uguali. Cosa ci rimane?
Rimangono il tetraedro, il cubo, l'ottaedro, il dodecaedro e l'icosaedro.
Ma la domanda è: esistono altri poliedri convessi regolari oltre a questi? Sarebbe legittimo pensare di sì; in analogia a quanto succede per i poligoni regolari (ce ne sono infiniti, e aumentando il numero dei lati ci si avvicina sempre di più a un cerchio) verrebbe da pensare che ci siano infinitii poliedri regolari e che, aumentando il numero delle facce, ci si avvicini sempre di più add una sfera. E invece?

Proviamo un po' a vedere.
Le facce devono essere poliedri regolari tutti uguali tra loro. Proviamo allora concretamente a vedere, utilizzando vari poligoni regolari di cartoncino, quali angoli solidi riusciamo a costruire. Intanto è chiaro che se mettiamo vicini 2 poligoni per un lato, creeremo un angolo diedro, ma non un angolo solido. Quindi dobbiamo mettere vicini almeno tre poligoni regolari uguali, in modo che abbiano un vertice in comune.
Con tre triangoli equilateri...
Mettiamo tre triangoli equilateri in modo che concorrano tutti in un vertice
 Ora chiudiamoli a formare un angolo solido
 Questo angolo è uguale a quelli del tetraedro
... formiamo l'angoloide che va bene per il tetraedro.
Con quattro triangoli equilateri...
Mettiamo quattro triangoli equilateri in modo che concorrano tutti in un vertice
 Ora chiudiamoli a formare un angolo solido
 Questo angolo è uguale a quelli dell'ottaedro
... formiamo l'angoloide che va bene per l'ottaedro.

Con cinque triangoli equilateri...
Mettiamo tre triangoli equilateri in modo che concorrano tutti in un vertice Ora chiudiamoli a formare un angolo solido
 Questo angolo è uguale a quelli dell'icosaedro
... formiamo l'angoloide che va bene per l'icosaedro.

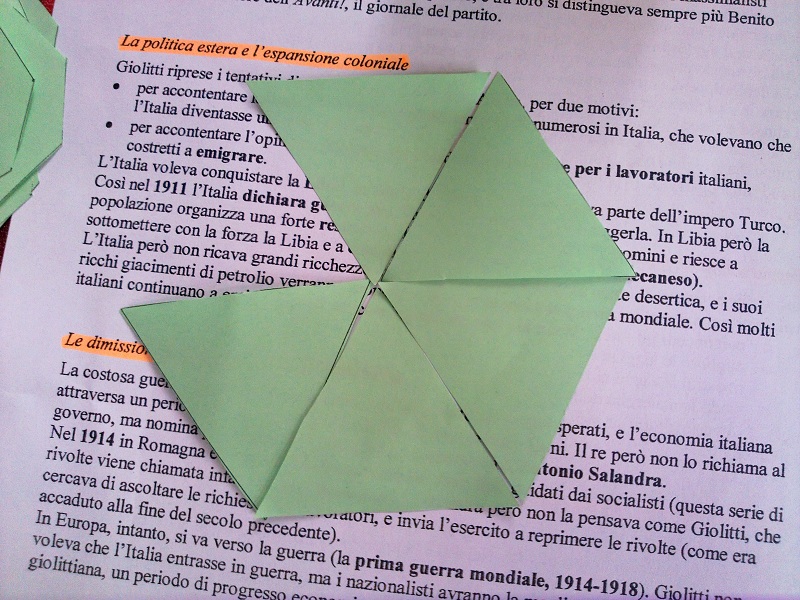
Con sei triangoli equilateri....
Mettiamo sei triangoli concorrenti in un vertice
... non si riesce a formare alcun angoloide (i triangoli sono spiaccicati sul piano!).

Con tre quadrati...
Mettiamo tre quadrati in modo che concorrano tutti in un vertice
 Ora chiudiamoli a formare un angolo solido
 Questo angolo è uguale a quelli del cubo
... formiamo l'angoloide che va bene per il cubo.

Con quattro quadrati...
Mettiamo quattro quadrati in modo che concorrano tutti in un vertice
... non si riesce a formare alcun angoloide (i quadrati sono spiaccicati sul piano!).

Con tre pentagoni regolari...
Mettiamo tre pentagoni regolari in modo che concorrano tutti in un vertice
 Ora chiudiamoli a formare un angolo solido
 Questo angolo è uguale a quelli del dodecaedro
... formiamo l'angoloide che va bene per il dodecaedro.

Con quattro pentagoni regolari...
Mettiamo tre pentagoni regolari in modo che concorrano tutti in un vertice
... non si riesce a formare alun angoloide (i pentagoni addirittura si sovrappongono sul piano!).

Con tre esagoni regolari...
Mettiamo tre esagoni regolari in modo che concorrano tutti in un vertice
... non si riesce a formare alun angoloide (gli esagoni sono spiaccicati sul piano!).

Con tre ettagoni regolari...
Mettiamo tre ettagoni regolari in modo che concorrano tutti in un vertice
... non si riesce a formare alun angoloide (gli ettagoni addirittura si sovrappongono sul piano!).

Con tre ottagoni regolari...
Mettiamo tre ottagoni regolari in modo che concorrano tutti in un vertice
... non si riesce a formare alun angoloide (gli ottagoni addirittura si sovrappongono sul piano!).

Riassumendo:
forma delle facce
 numero delle facce
concorrenti in un vertice
 angolo interno
di una faccia
 somma degli angoli
concorrenti in un vertice
 poliedro corrispondente
triangolo equilatero
 3
 60°
 180°
 tetraedro
4
 240°
 ottaedro
5
 300°
 icosaedro
6
 360°
 ---
quadrato
 3
 90°
 270°
 cubo
4
 360°
 ---
pentagono regolare
 3
 108°
 324°
 dodecaedro
4
 432°
 ---
esagono regolare
 3
 120°
 360°
 ---
ettagono regolare
 3
 128,57° circa
 385,71°
 ---
ottagono regolare
 3
 135°
 405°
 ---

Poiché aumentando il numero dei lati del poligono aumenta l'ampiezza dell'angolo interno delle facce (e, ovviamente, aumentanddo il numero delle facce, aumenta la somma degli angoli concorrenti in un vertice) non si possono costruire altri poliedri regolari convessi: quando la somma degli angoli concorrenti in un vertice eguaglia (o supera) l'angolo giro (360°), non si riesce più a creare l'angolo solido, non si riescono più a chiudere le facce, e quindi non si possono creare altri poliedri regolari.

Per approfondire e ripassare, puoi guardare anche questa pagina di Base Cinque, o questa pagina di Matematita.
In questa pagina puoi trovare curiosità storiche e una bella applet per visualizzare i poliedri in movimento e come si possono includere uno nell'altro.
Se vuoi anche esercitarti un po' con l'ingelse, potresti invece guardare questo video (in due parti):




Torna alla pagina iniziale del laboratorio sui poliedri