Comprensione del problema

«Non ha senso rispondere ad una domanda che non si è compresa. È duro lavorare per uno scopo che non si desidera. Simili cose sciocche e tristi tuttavia accadono spesso, nella scuola e fuori dalla scuola; ma un buon insegnante dovrebbe sforzarsi di impedire che esse si verifichino nella sua classe. Lo studente dovrebbe capire il problema e, di più, dovrebbe considerare di conoscerne la soluzione. Non è sempre tutta colpa dell'alunno se questa comprensione e questo desiderio mancano; i problemi dovrebbero essere scelti con cura, né troppo difficili né troppo facili, semplici ed interessanti; e spesso essi dovrebbero essere presentati in una forma gradevole, piana e atta a risvegliare la curiosità dei giovani.»
[Polya 1945, pagg. 25 e seg.]

Comprensione del testo

Una prima questione, a mio parere, riguarda la formulazione dei testi dei problemi. I ragazzi conoscono il significato da noi attribuito a tutte le parole che utilizziamo? Ne dubito, dopo aver visto alcune delle difficoltà degli studenti di IV! "Colpa" degli alunni, che non stanno attenti, che si distraggono, che leggono senza soffermarsi sulle parole o senza dare a tutte il giusto peso, ma forse anche "colpa" di noi insegnanti, che non sempre esplicitiamo tutto. Vorrei fare di seguito degli esempi, che potrebbero scandalizzare i matematici di professione, ma che credo non si allontanino troppo da ciò che succede nelle nostre classi.
Vediamo alcuni esempi tratti dai problemi proposti su Matematica contro luce, iniziando con alcuni dei termini comunemente utilizzati.

inscrivere	Sicuramente ai ragazzi è stata data la definizione di poligono inscritto ad una circonferenza. Non sono tanto sicura che questo basti per dire che la richiesta di inscrivere un poligono in una circonferenza non crei ambiguità. Anzi, credo proprio che, anche appena data la suddetta definizione, se facciamo ai ragazzi una tale richiesta, alcuni di essi disegneranno semplicemente un poligono interno alla circonferenza.
circoscrivere	Analogamente, anche se è data la definizione di poligono circoscritto, non è immediato per i ragazzi sapere con esattezza che cosa intendiamo chiedere loro quando diciamo di circoscrivere ad una circonferenza un certo poligono.
unitario	Alcuni ragazzi (questo l'ho direttamente verificato nel tirocinio) non sanno che "segmento unitario" sta per "segmento di misura una unità"; rispetto a tale precisazione o si bloccano perché non capiscono o proseguono ancora per poco, perché non sanno rispetto a cosa indicare le misure degli altri elementi del problema.
staccare	Quando una curva ha due intersezioni distinte con una retta diciamo che essa stacca sulla retta il segmento che ha per estremi le due intersezioni; non credo però che questa definizione compaia sui libri di testo. Siamo sicuri che tutti i ragazzi danno a questo verbo il significato inteso da noi?
generico	In questo caso, oltre a non essere sicura che questo aggettivo sia chiaro ai ragazzi, mi chiedo anche se sia una scelta veramente felice. Dà l'idea di variabile o semplicemente di preso a caso, ma, una volta preso, fissato?
distanza	Non c'è dubbio che i ragazzi sappiano (e si ricordino) che cos'è la distanza tra due punti. Ma siamo sicuri che tutti sappiano (o si ricordino) che cos'è la distanza tra un punto e una retta o la distanza tra due rette?
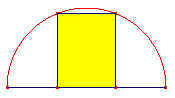
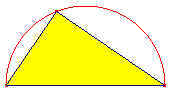
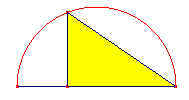
inscritto	Se questo è un rettangolo inscritto in una semicirconferenza...	... perché un triangolo rettangolo inscritto in una semicirconferenza deve essere per forza così...	... e non può essere invece così?

Un altro dubbio, relativamente alla comprensione dei problemi da parte dei ragazzi, mi sorge riguardo a certi costrutti.
Primo fra tutti, quello che spesso in matematica serve per brevità, caratterizzato da quel fatidico "... rispettivamente..." a volte persino sottinteso:

Altro costrutto che i ragazzi faticano a capire è quello in cui si utilizzano pronomi che grammaticalmente potrebbero riferirsi a nomi diversi; per noi il contesto geometrico risolve l'ambiguità; ma per loro, che cosa risolve l'ambiguità se deve essere il testo a chiarire il contesto geometrico?

Non dico che tutte queste espressioni andrebbero bandite. Si rischierebbe una grossa perdita di agilità e non si avvicinerebbero mai i ragazzi a quello che è il "gergo" (oltre che il linguaggio) dei matematici. Ma non credo sia buona cosa dare per scontata la comprensione di ciò che diciamo, o almeno non all'inizio.
Un suggerimento che Polya dà al riguardo è quello di chiedere agli studenti di ripetere l'enunciato; forse così, davvero, potremo avere almeno il dubbio che il nostro testo non sia troppo ambiguo!

Scelta della variabile

Nella comprensione del problema, Polya fa rientrare la scelta dell'incognita. Giustamente, rispetto ai problemi presentati nella sua opera, egli parla di incognita (per i problemi di determinazione) o di tesi (per i problemi di dimostrazione). Comunque suggerisce di non perdere di vista ciò che si vuole ottenere, di riflettere su di esso, per trovare (ad esempio) problemi già risolti in cui si cercasse lo stesso elemento in un'altra figura, o teoremi già dimostrati in cui si volesse arrivare alla stessa tesi a partire da altre ipotesi.

Tutte queste riflessioni (si veda [Polya 1945] alle pagg. 129 e segg.) sono utili anche per i problemi di cui ci stiamo occupando e sarebbe opportuno farle con i ragazzi, stando però attenti, dal mio punto di vista, a operare una "leggera" modifica, peraltro trascurata sia da Matematica uno che da Matematica controluce. Nei problemi di cui si sta trattando, infatti, non c'è una incognita, bensì una variabile. Non credo sia solo una sottigliezza di un'appassionata di logica...
Se chiedo ad un ragazzo il più banale problema di questo tipo, ad esempio, se gli chiedo di esprimere in funzione del lato AB di un quadrato la sua area, credo che non avrebbe grosse difficoltà. Ma se, dopo averglielo chiesto, gli dico subito che AB è l'incognita del problema... o il ragazzo è uno di quelli che ascoltano poco gli insegnanti, oppure non saprà come procedere. Se voglio aiutarlo, invece che confondergli le idee, potrò invece dirgli che AB è la variabile (indipendente) del problema, rispetto alla quale si vuole dire come varia l'area del quadrato (variabile dipendente).

Disegnare una figura

Giungiamo, a questo punto, ad una questione che ritengo abbastanza delicata e qui particolarmente rilevante, in vista anche del tipo di attività che è stata proposta durante il mio tirocinio: il ruolo della figura nella risoluzione dei problemi di geometria.
Ricorderò sempre il mio imbarazzo quando il prof. Marchi mi colse, durante una lezione di Matematiche complementari all'Università, tutta intenta nel cercare di fare un "bel disegno" relativamente a non so più quale teorema;  non se la prese più di tanto, devo dire, ma nemmeno mi risparmiò la ramanzina sul fatto che "La geometria è l'arte di fare i ragionamenti giusti sulle figure sbagliate". Non lo dimenticherò mai, fosse anche solo per la situazione in cui me lo sono sentito dire!
A parte i dolci ricordi dell'Università, sono d'accordo sul fatto che elemento portante in geometria deve essere la deduzione e che questa avviene nel nostro pensiero e non su un foglio di carta: «la figura disegnata non è fondamento di conclusione rigorosa; questa deve invece essere affidata esclusivamente al ragionamento coerente» [Manara, Marchi 1993, pag. 53]. Del resto già il Polya, che pure inserisce il tracciamento della figura tra i punti fondamentali per la comprensione di un problema (si vedano le pagg. 111 e segg. di [Polya 1945]), sottolinea che «la figura serve come ausilio, ma, per nessun motivo, come fondamento per i risultati che si conseguono; questi si basano esclusivamente sulle connessioni logiche intercedenti tra di essi» [Polya 1945, pag. 114].
Il ruolo della figura, a mio parere, è quello di aiutare l'immaginazione, ossia quel momento in cui non si vuole ancora dimostrare, ma si sta cercando che cosa dimostrare; non si vuole ancora calcolare, ma si sta cercando che cosa calcolare; non si vuole ancora procedere, ma si sta cercando la direzione.

Per risolvere un problema mi pare di poter dire che queste due facoltà, quella razionale e quella immaginativa, siano necessarie entrambe. Ma insegnare ai ragazzi a ragionare è possibile? Se anche lo fosse, è possibile insegnare ai ragazzi ad immaginare?

La prof.ssa Raffaella Manara, in un corso di perfezionamento, ci fece riflettere sul fatto che si può insegnare a ragionare in tanto in quanto si può educare i ragazzi a "riflettere sul proprio pensiero", a sviluppare il proprio "livello di consapevolezza" (si veda [Manara 1999]). Così, credo, che si possa non tanto insegnare ad immaginare quanto rendere coscienti i ragazzi delle proprie potenzialità immaginative. L'uso di CabriGéomètre serve proprio a questo. Fin tanto che i ragazzi hanno sempre e solo visto figure statiche, come fanno ad attivare la loro facoltà di immaginare figure in movimento? Magari qualcuno ce la fa immediatamente, ma gli altri? E soprattutto: come faccio io insegnante a capire che i miei ragazzi stanno figurandosi in mente ciò che anch'io ho in mente? Come posso sapere se stanno ricostruendo nel proprio pensiero esattamente la figura variabile descritta dal testo del problema? Cabri mi può essere utile per far capire ai ragazzi che sono "autorizzati" ad immaginarsi, quando sentono parlare di un triangolo inscritto in una semicirconferenza, non un unico triangolo, non semplicemente un triangolo qualsiasi tra tutti i possibili, ma un'intera famiglia di triangoli, che si trasformano uno nell'altro mantenendo invariate alcune proprietà ma mutandone altre.

Non c'è dubbio che l'uso di CabriGéomètre, come del resto di qualsiasi altro strumento, debba essere fatto in modo molto attento. Il rischio, credo, è che invece di stimolare l'immaginazione dei ragazzi la si blocchi, perché "tanto c'è Cabri" che lavora per loro. Come cogliere i vantaggi dell'uso di Cabri senza correrne i rischi?
Innanzitutto credo che l'uso di questo software debba essere limitato nel tempo: è all'inizio che devo assicurarmi di riuscire a comunicare ai ragazzi che cosa intendo per "punto che si muove" su un certo vincolo; è all'inizio che devo trovare il modo per farli accorgere di questa possibilità della loro immaginazione; una volta avviato il processo, Cabri non deve più servire.
In secondo luogo deve essere chiaro l'atteggiamento dell'insegnante nei confronti del valore del software. Non può essere usato come strumento di controllo, ad esempio, per vedere se le nostre congetture riguardo ai casi limite erano corrette; è solo il nostro ragionamento che le può convalidare. I ragazzi devono veder l'insegnante usare Cabri come una lavagna, sulla quale egli scrive ciò che vuole, ciò che egli stesso (e non Cabri) ha deciso. Semplicemente, si deve trattare di una lavagna dinamica, attraverso la quale l'insegnante riesce a comunicare ciò che vuole in modo più efficace, grazie a dei simboli in movimento.
Inoltre la figura di Cabri deve essere mostrata solo dopo aver lasciato il tempo ai ragazzi di immaginarsi qualcosa; essa diventa allora non tanto un controllo sul ragionamento, ma un controllo sul fatto di essersi immaginati tutti la stessa cosa e di poter iniziare a ragionare attorno alla stessa immagine mentale. Proporre la figura di Cabri subito dopo aver dettato il testo di un problema, significherebbe relegare i ragazzi ad un ruolo passivo, che è esattamente il contrario di ciò che ci si vuole.
Infine credo che Cabri possa, da un certo punto in poi, essere utilizzato in modo diverso da studenti diversi. Quando lo ritenesse opportuno, ad esempio, l'insegnante potrebbe affidare ai più brillanti la preparazione delle figure fatte con Cabri, da utilizzare eventualmente nella lezione successiva come aiuto per i ragazzi che non siano riusciti a risolvere i problemi, perché bloccatisi di fronte alla costruzione della figura.

Una parola ancora, a mio parare, va spesa riguardo all'uso di Cabri per evidenziare il legame tra la figura iniziale e il grafico della funzione che il problema propone di studiare. Il procedimento che si richiede ai ragazzi è quello di passare dall'osservazione di certe proprietà geometriche della figura iniziale alla formulazione di una relazione algebrica, e poi da questa alla sua rappresentazione grafica. In questo modo, ciò che lega la figura al grafico è l'equazione, ricavata dalla prima e usata per ricavare il secondo. Utilizzando Cabri come è stato fatto, questo passaggio si evita. Ora, non è che si voglia (e nemmeno si possa) insegnare ai ragazzi ad evitare questo passaggio, anche perché non sarebbe affatto utile una volta che si fosse privi del software.
Anche in questo caso Cabri serve piuttosto per far capire ai ragazzi che essi possono (o devono) immaginarsi anche i grafici in modo dinamico.
Non è così banale passare dalla concezione di parabola come luogo geometrico inserito in un sistema di riferimento a quella di parabola come grafico di una funzione. Nel primo caso, i punti della parabola sono alcuni dei punti del piano, scelti in modo da rispettare determinate proprietà; questi punti costituiscono tutti insieme il luogo geometrico e per un po' abituiamo i ragazzi a pensarli come un tutt'uno, tra l'altro "indipendente" dal sistema di coordinate scelto: la parabola è la parabola, poi posso decidere di inserirla in un sistema di riferimento e vedere che tipo di coordinate hanno i suoi punti. Nel secondo caso, le cose cambiano notevolmente; l'idea è che si ha fin da subito un sistema di riferimento e in esso si vanno ad evidenziare tutti i punti le cui coordinate soddisfano un certo legame, tutti i punti la cui ordinata è in una certa relazione con la rispettiva ascissa. Qui è insita l'idea di variabilità e di movimento che nello studio delle coniche in quanto tali non emerge. Prendere sottogamba questo fatto implica a mio parere delle difficoltà enormi che riemergono, solitamente, nell'ultimo anno di corso, quando si iniziano a studiare i limiti delle funzioni reali a variabile reale. Per alcuni ragazzi, non abituati a immaginare i punti che si muovono sul grafico delle funzioni, il nostro dire "dove va la y quando la x va a ...?" non ha alcun senso e quindi non li aiuta a capire il concetto di limite; credo che ciò sia attribuibile al fatto che non li si è mai abituati a immaginare "la y che va da qualche parte", non li si è mai autorizzati a pensare il grafico se non come un disegno statico di qualche cosa.
Di nuovo, per i ragazzi più brillanti si apre una ulteriore possibilità. La costruzione del grafico della funzione ricercata nel problema è "banale" quando si tratta di un perimetro o comunque della misura della somma o della differenza tra segmenti, o tra multipli di segmenti. È tutt'altro che banale, invece, quando si tratta di moltiplicare tra loro le misure dei segmenti o di dividerne una per un'altra. Far fare ai ragazzi questa costruzione (non a tutti, si intende, ma a coloro per i quali ad un certo punto la risoluzione dei problemi è già diventato un puro esercizio, una pura ripetizione) implica insegnargli ciò che noi abbiamo imparato solo all'università, ma che da solo può far veramente concepire la grandezza della geometria analitica. Utilissimo sarebbe, a mio parere, farglielo apprendere direttamente leggendo le primissime pagine della Geometria di Cartesio. ma qui si aprirebbe tutto un altro discorso, che va ben al di là del nostro immediato interesse...!