| ENIGMA 102 Luca L. 21 maggio 2007 [soluzioni] |
0 0 0 =6 1 1 1 =6 2 2 2 =6 3 3 3 =6 4 4 4 =6 5 5 5 =6 6 6 6 =6 7 7 7 =6 8 8 8 =6 9 9 9 =6 Mettere opportune operazioni matematiche tra i simboli scritti in modo che il risultato sia ogni volta 6. E' consentito usare parentesi e altri numeri ma solamente agli eventuali esponenti. Non è consentito applicare delle operazioni agli esponenti. |
| ENIGMA 101 Elisa A.M. 14 maggio 2007 [soluzioni] |
Immaginate di avere un foglio di carta
rettangolare spesso un decimo di millimetro e grande a piacere (come epsilon è
piccola...ih ih ih). Ora piegatelo a metà in modo da ottenere due mezzi fogli
sovrapposti, quindi con uno spessore doppio. Continuate poi a piegare in due, ottenendo
via via fogli sempre più piccoli e spessori maggiori. Dopo 42 piegamenti, immaginate di
salire sulla torre di carta che avete creato. Secondo voi di quanto vi potete innalzare? 1) Riuscite appena a fare uno scalino (circa 20 cm) 2) Arrivate al primo piano di una casa (circa 3 m) 3) Potete conquistare la cima dell'Everest (circa 8800 m) 4) Sarete il primo piegatore di carta sulla Luna (circa 385000 km) |
| ENIGMA 100 Marco D.V. 8 maggio 2007 [soluzioni] |
Usando tutte le dieci cifre disbonibili in base
10 (ovvero 0,1,......,9) si scrivi un numero di dieci cifre tale che: il numero ottenuto considerando le prime k cifre da sinistra sia divisibile per k con k che va da uno a dieci. In modo più semplice:la prima cifra a sinistra sia divisibile per uno, le prime due da sinistra siano divisibili per due,........,ed il numero intero deve essere disibile per 10. |
| ENIGMA 99 Luca B. 30 aprile 2007 [soluzioni] |
La rosa della mortalità (enigma_99.pdf) |
| ENIGMA 98 Sara D.M. 23 aprile 2007 [soluzioni] |
Trovare un numero intero tale che spostando la prima cifra dopo l'ultima si ottenga la metà esatta del numero dato. |
| ENIGMA 97 Sofia S. 17 aprile 2007 [soluzioni] |
Clara e sua zia Matta Matica sono all'ospizio
militare di Chelsea e vedono passare lunghe file di stagionati eroi... "Che cosa triste, tristissima!" esclamo' Clara; e gli occhi della cara fanciulla si empirono di lacrime mentre pronunciava queste parole. "Triste, ma abbastanza interessante se la si prende in esame da un punto di vista aritmetico", fu la poco romantica risposta della zia. "Diciamo che il 70 per cento abbia perso un occhio, il 75 per cento un orecchio, l'80 per cento un braccio, l'85 per cento una gamba.Ora, cara, che percentuale, al minimo, deve aver perso tutte e quattro le parti del corpo?" (liberamente tratto da Lewis Carrol, I garbugli del reverendo) |
| ENIGMA 96 Giovanni V. 12 aprile 2007 [soluzioni] |
Un signore sta guidando la sua macchina quando,
osservando il contachilometri, si accorge che segna 15951 km, che è un numero palindromo, cioe`un numero che letto da destra a sinistra o da sinistra a destra resta invariato. "Che strano", dice a se stesso "chissà quanto tempo ci vorrà prima che questo accada di nuovo!" Ed invece dopo sole 2 ore il contachilometri segna un altro numero palindromo. A che velocità media ha viaggiato l'automobilista in queste 2 ore? |
| ENIGMA 95 Silvia P. 3 aprile 2007 [soluzioni] |
La squadra di matematica del liceo Moretti (che è composta, almeno per stavolta, non da 7 ma da 10 persone) si sta recando a Cesenatico per disputare la finale nazionale, quando viene rapita da un gruppo di matematici inferociti. Costoro dispongono i ragazzi in fila indiana e in ordine di altezza, in modo che il ragazzo più alto riesca a vedere tutti gli altri, il secondo più alto veda tutti tranne il primo e così via fino al più basso che non vede nessuno. A ciascun ragazzo viene messo in testa un cappello, bianco o nero. I carnefici vanno poi dal ragazzo più alto e gli chiedono quale sia il colore del suo cappello: se indovina, lo lasciano andare; se sbaglia, lo costringono a impararsi a memoria i numeri primi da uno a un miliardo. Poi passano al successivo e ripetono la stessa domanda; e così via fino all'ultimo. Dato che nessun ragazzo muore dalla voglia di imparare tutti questi numeri e dato che erano al corrente del metodo utilizzato dalla banda, hanno escogitato un piano che consente di salvare per certo il massimo numero di persone. I ragazzi non possono comunicare tra loro con gesti o altro, possono solo rispondere "bianco" o "nero" quando i carnefici pongono la domanda. Come possono fare? |
| ENIGMA 94 Fulvia S.R. 26 marzo 2007 [soluzioni] |
L’enigma si occupa di venusiani e di un progetto che stanno realizzando. Per portare l’acqua in ogni zona di Venere, gli abitanti hanno circondato l’equatore del loro pianeta con una lunga conduttura. Purtroppo però, a lavoro quasi ultimato, alcuni hanno deciso di modificare il progetto di partenza, perché ritengono sia meglio sollevare la conduttura dell’acqua a due metri di altezza. Ovviamente è nata una discussione tra chi è favorevole alla modifica e chi no. Per risolvere la questione, prima di rifare tutto il lavoro e di affrontarne i nuovi costi, vogliono sapere di quanto è necessario allungare la conduttura. Ora, io non so quanto sia lungo il loro equatore e non so come aiutarli a trovare la risposta. Mi date una mano voi? |
| ENIGMA 93 Paolo C. 20 marzo 2007 [soluzioni] |
Paolo sta cercando casa. L'agente immobiliare
Lucifero gli propone una abitazione a forma di triangolo equilatero immersa in un bel
giardino pure a forma di triangolo equilatero, in modo che il il triangolo della casa sia
inscritto nella stessa circonferenza in cui il triangolo del giardino è circoscritto. Per
capire si veda la figura: Lucifero sa che l'abitazione misura 100 mq (commerciali), ma non sa dire l'estensione del giardino. Paolo sì: senza fare troppi calcoli, sa esattamente quanto vale la superficie del giardino. Quanto vale l'area del giardino, e come fa Paolo ad ottenerla in modo diciamo così... elegante? |
| ENIGMA 92 Michela E. 9 marzo 2007 [soluzioni] |
Michela si è innamorata perdutamente di un
bellissimo ragazzo tedesco. Purtroppo non ha ancora capito se lui "ci è" o
"ci fa" quindi per ora si accontenta di sospirare pensando intensamente
"M'ama o non m'ama?". Siccome a Berlino fa ancora freddino e non ci sono
margherite da sfogliare, Michela fa il seguente gioco: ogni giorno costruisce una tabella
quadrata 4 * 4 (quattro per quattro) e in ciascuna delle caselle della tabella scrive la
cifra 1 oppure la cifra 2. La cifra 1 sta per "M'ama" la cifra 2 sta per
"Non m'ama". Ha convenuto che la somma delle 9 cifre contenute in ciascuno dei 4
quadrati 3 * 3 (tre per tre) contenuti nella tabella iniziale deve essere multipla di 4,
mentre la somma di tutte le 16 cifre non deve essere multipla di 4. Alla fine della
giornata fa la somma delle 16 cifre e se viene fuori un numero dispari vuol dire che quel
giorno lui la ama, altrimenti vuol dire che quel giorno lui non la ama. Michela vi chiede
di determinare il massimo valore e il minimo valore possibile per la somma di tutte le 16
cifre P.s. probabilmente se il ragazzo tedesco venisse a conoscenza del passatempo di Michela, se ne scapperebbe a gambe levate lasciandola sola con i suoi numeri... |
| ENIGMA 91 Stefano P. 28 febbraio 2007 [soluzioni] |
Il piccolo gigetto (ma dai?!?), come ben
sappiamo, ama molto i giochi e i giochini, di qualsiasi natura siano. E soprattutto ama
vincere. E allora sfida gli amici a questo gioco: su una calcolatrice digita il numero
616, poi espone le regole: i due giocatori, a turno, possono solo sottrarre dal numero
visualizzato 1,2,3,4,5,6,7,8,9 o 10 a loro scelta. Vince il primo giocatore che riesce a
far comparire 0 sul display della calcolatrice. Poi, visto che è generoso, concede la prima mossa al suo avversario... ma inspiegabilmente riesce sempre a vincere... perché? |
| ENIGMA 90 Marco D.V. 29 gennaio 2007 [soluzioni] |
Le figure che vedete qui sotto sono entrambe
composte da: a) un triangolo rettangolo rosso 8x3; b) un triangolo rettangolo rosa 5x2; c) una figura gialla imprecisata; d) un'altra figura imprecisata...ma questa volta è azzurra; La domanda è: come è possibile che nel secondo disegno avanzi un buco?  |
| ENIGMA 89 Luca B. 15 gennaio 2007 [soluzioni] |
PRESE DOVE MISE MISE MISE MISE MISERO MISERO MISE
MISERO PRESE PRESE TRE. Dare un significato alla frase, aggiungendo unicamente i segni di interpunzione. |
| ENIGMA 88 Sara D.M. 8 gennaio 2007 [soluzioni] |
Un
pomeriggio nascono 2 gemelli a distanza di 30 minuti l'uno dall'altro. Luigi nasce per
primo e Alessandro per secondo, ma Alessandro festeggia il complenno sempre un giorno
prima di Luigi e in alcuni casi addirittura due giorni prima. Come è possibile? |
| ENIGMA 87 Sofia S. 11 dicembre 2006 [soluzioni] |
Un monaco buddista si reca a meditare sulla
montagna, partendo all'alba dal convento. Durante la marcia, il monaco si ferma a mangiare
e alcune volte a riposare. Arriva sulla cima della montagna nel tardo pomeriggio e inizia
il periodo di meditazione. Dopo alcuni giorni, riparte all'alba per rientrare al convento,
dove arriva nel pomeriggio dopo aver percorso la stessa strada della salita. Si accorge che esiste un punto lungo il percorso in cui, durante i viaggi, è passato alla stessa ora. In che condizioni è possibile questo? |
| ENIGMA 86 Giovanni V. 27 novembre 2006 [soluzioni] |
Un tale con 6 pezzi di catena di 5 maglie ciascuno vuol farci una collana e decide quindi di portarli da un gioielliere per farli unire. Il gioelliere gli chiede un compenso di 10 euro per ogni maglia che apre e chiude. La collana viene a costare 60 euro, ma il cliente non è d'accordo perché secondo lui si può spendere meno. Quanto? |
| ENIGMA 85 Luca L. 20 novembre 2006 [soluzioni] |
7 nomi di 7 grandi matematici sono
crittografati come segue: 1) UENOBN 2) UBTSSP 3) FBNOZV 4) GITUFD 5) DVCULB 6) DEPETB 7) DETVTD. Si chiede di decifrare i 7 nomi sapendo che ...... una certa semplice frazione legata al numero 7 fornisce la "chiave". |
| ENIGMA 84 SIlvia P. 13 novembre 2006 [soluzioni] |
Scrivere il numero 100 attraverso la somma di 5 numeri, non necessariamente interi, utilizzando una ed una sola volta tutte e dieci le cifre da 0 a 9.Naturalmente può esserci più di una soluzione: stupitemi con la vostra creatività! |
| ENIGMA 83 Fulvia S.R. 30 ottobre 2006 [soluzioni] |
Angelo, Bruno, Carlo, Davide ed Enrico hanno
appena cambiato l'auto; le macchine sono blu, gialla, nera, rossa e verde e delle seguenti
marche: Citroen, Fiat, Honda, Renault e Toyota. La più economica è costata 9.000 euro,
la seconda 10.000, quindi 11.000, 12.000 e 13.000. La Fiat non è gialla, Angelo ha comprato una Renault. L'auto di Bruno non è una Toyota ed è la più economica. Carlo voleva comprare una Citroen, ma ha preferito risparmiare. Davide ha scelto la vettura nera, chi ha scelto la Toyota preferisce il blu. La Citroen non è nera, l'auto rossa costa meno della Honda, ma più di quanto ha speso Enrico. Stabilire il colore, la marca e il prezzo dell'auto comprata da ciascuno degli amici. |
| ENIGMA 82 Elisa A.M. 23 ottobre 2006 [soluzioni] |
5 2 9 8
4 6 7 3 1 0 Sono i numeri, da 0 a 9 (per chi non li avesse riconosciuti). In che ordine sono? |
| ENIGMA 81 Michela E. 16 ottobre 2006 [soluzioni] |
Juergen (tipico nome tedesco) torna dalla pesca con una borsa piena di pesci. Giunto a casa, dà al più grande dei suoi due gatti i tre pesci più grossi: così facendo il peso della borsa si riduce del 38%. A questo punto dà all'altro gatto i tre pesci più piccoli: così facendo il peso della borsa si riduce nuovamente del 38% - questo però rispetto al peso successivo alla nutrizione del primo gatto. Quanti pesci ha pescato Juergen? (si trascuri il peso della borsa rispetto a quello dei pesci). |
| ENIGMA 80 Anita P. 9 ottobre 2006 [soluzioni] |
Due amiche con la passione per l'enigmistica si
incontrano per caso dopo diversi anni e decidono di fare una passeggiata insieme. Ad un certo punto Sara dice all'amica: "Quindi hai tre figlie... E quanti anni hanno?" "Il prodotto delle loro età è pari a 72." Risponde Martina. Sara ci pensa un po' e poi dice: "Ci sono varie combinazioni di tre numeri che hanno come prodotto 72. Dammi un aiutino." "Vedi l'autobus che arriva? Il suo numero è uguale alla somma delle loro età." Risponde Martina. Sara guarda il numero dell'autobus riflette un pò e poi afferma: "Non mi hai dato informazioni sufficienti per trovare una risposta univoca." "E' vero" commenta Martina" però ti dico che se oggi non ci fossimo incontrate ed il nostro primo incontro fosse avvenuto solo tra un anno ed io, in tale circostanza, avessi risposto alle tue precedenti domande in modo corretto, ebbene tu anche in questa occasione non avresti potuto indovinare le loro età!" A quel punto Sara è in grado di dare la risposta giusta. Com'è possibile? NB: tutte le figlie hanno almeno un anno. |
| ENIGMA 79 Paolo C. 2 ottobre 2006 [soluzioni] |
Mio zio Geppo possiede una tenuta tutta coltivata
a tuberi non specificati. La superficie coltivabile del campo misura 1000 metri quadrati.
Un bel giorno lo zio decide di recintare la tenuta, va al mercato e compra 100 metri di
recinto. Torna a casa e la moglie gli dice: "Mio caro Geppetto, avresti fatto meglio
a comprare qualche metro in più!". Tuttavia la mattina seguente Geppetto si mette al
lavoro e riesce a recintare tutto il suo campo utilizzando solamente i 100 metri di recinto comprati il giorno prima. Come è possibile? |
| ENIGMA 78 Stefano P. 25 settembre 2006 [soluzioni] |
Due ragazze si sono appena trasferite a Trento dove intendono trascorrere i successivi 3/5 anni studiando per una laurea in Sociologia, e hanno deciso di prendere appartamento insieme. Ovviamente appena arrivate hanno tutta la casa da sistemare... e in particolare oggi si sono dedicate alla sistemazione e pulizia della cantina. Al termine del lavoro la cosa singolare è che Guendalina ha il viso tutto sporco, mentre Genoveffa ha il viso bello pulito (sarà indizio di chi ha veramente lavorato per pulire la cantina?). Ma la cosa ancora più singolare è che, dopo aver ammirato con soddisfazione la cantina in ordine, Genoveffa decide di andare di filato in bagno a farsi una doccia, mentre Guendalina, senza nemmeno ripulirsi, decide di uscire a fare shopping. A voi dirmi: perché questo strano comportamento? [Attenzione: Guendalina non ha il viso sporco perché si è, per esempio, truccata in vista del pomeriggio di shopping. La sporcizia sul viso è proprio sporcizia, originata dal lavoro di pulizia della cantina.] |
| ENIGMA 77 Luca B. 20 giugno 2006 [soluzioni] |
È possibile scrivere il numero 100 (il n umero è in base 10) in almeno quattro modi differenti usando ogni volta solo una cifra ripetuta per cinque volte? (Ovviamente la risposta è sì). Trovatemi questi quattro modi, se ce la fate.... |
| ENIGMA 76 Sara D.M. 13 giugno 2006 [soluzioni] |
Con
quale coppia di lettere deve proseguire logicamente la seguente serie: |
| ENIGMA 75 Sofia S. 6 giugno 2006 [soluzioni] |
Un bicchiere di limonata, tre sandwiches e sette
biscotti costano 1 scellino e 2 pence (che significa 14 pence, visto che 1 scellino
equivale a 12 pence). Un bicchiere di limonata, 4 sandwiches e 10 biscotti costano 1 scellino e 5 pence. Quanto costano un bicchiere di limonata, un sandwich e un biscotto (nel complesso)? E quanto costano (sempre nel complesso) due bicchieri di limonata, tre sandwiches e 5 biscotti? |
| ENIGMA 74 Giovanni V. 30 maggio 2006 [soluzioni] |
Un poverello non riusciva a rinunciare al vizio del fumo. Non avendo abbastanza soldi per acquistare le sigarette raccoglieva i mozziconi e riusciva costruirsi con cinque di essi una sigaretta. Un giorno riuscì a fumare cinque sigarette sfruttando questo espediente. Quanti mozziconi ha dovuto raccogliere quel giorno e quanti gliene sono avanzati? |
| ENIGMA 73 Luca L. 8 maggio 2006 [soluzioni] |
Enrico è uno studente molto appassionato di
Logica. Una sera uscì con la sua fidanzata e le disse: "Ti voglio chiedere un favore: io pronunzierò una frase, e tu mi devi promettere che, se la frase è vera, mi regalerai una tua fotografia; mentre, se la frase è falsa, mi devi promettere che non mi regalerai affatto la tua fotografia". "D'accordo", rispose la ragazza. Ed Enrico pronunziò una frase tale che la ragazza, dopo una breve riflessione, capì con sorpresa e mal celato divertimento, che se voleva mantenere la parola data, avrebbe dovuto dare ad Enrico non solo la sua foto, ma anche ... un bacio! Quale frase pronunziò Enrico? |
| ENIGMA 72 Silvia P. 1 maggio 2006 [soluzioni] |
Un giorno, camminando vicino alla
zona industriale di Sarezzo, mi sono imbattuta in uno strano essere tutto verde. Sulle
prime ho pensato potesse essere una trota con mutazioni genetiche dovute a tutte le
schifezze che gettano nel Gobbia, poi l'essere mi ha spiegato di essere un marziano, in
particolare un marziano matematico (ma guarda che combinazione!). Per verificare che fosse
vero, gli ho proposto di risolvere una semplice equazione: x^2 - 16x + 41 = 0 Per tutta risposta, il marziano mi ha detto che la differenza delle radici dell'equazione è 10. La domanda è: quante dita ha il marziano? |
| ENIGMA 71 Paolo P. 26 aprile 2006 [soluzioni] |
C'e una formica che si muove sul reticolo
seguente: 0 - 0 - 0 - 0 - 0 | | | | | 0 - 0 - 0 - 0 - 0 | | | | | 0 - 0 - 0 - 0 - 0 | | | | | 0 - 0 - 0 - 0 - 0 | | | | | 0 - 0 - 0 - 0 - 0 Gli 0 sono i nodi, - e | i collegamenti tra i nodi. La formica parte dal nodo in basso a sinistra e deve raggiungere quello in alto a desta con il vincoli seguenti: 1. in ogni percorso ci cono 4 collegamenti alto-basso (U) e 4 sinista-destra (D) 2. i percorsi che costeggiano interamente i lati del reticolo non sono ammessi (UUUUDDDD e DDDDUUUU non sono ammessi). Nel centro del reticolo c'è un chicco di grano. Domanda: prendendo un cammino a caso fra quelli consentiti, qual è la probabilità che la formica trovi il chicco? Nota: i cammini consentiti sono equiporbabili. |
| ENIGMA 70 Fulvia S.R. 10 aprile 2006 [soluzioni] |
Quattro coppie di amici si sfidano a tennis. Per
formare le coppie per il doppio misto, decidono di distribuire alle donne le quattro
regine di un mazzo di carte, ai mariti i quattro re, con l’intesa che giocheranno
insieme l’uomo e la donna che hanno re e regina dello stesso seme. Si siedono intorno
a due tavoli, le donne divise dagli uomini, in modo che i due componenti di una coppia
nella vita abbiano lo stesso orientamento rispetto agli altri: quindi marito e moglie
siedono entrambi a Nord, Est e così via. Prima di distribuire le carte, decidono che gli
uomini che hanno una carta rossa diranno la verità, quelli che hanno una carta nera
mentiranno; le donne invece stabiliscono che saranno tutte sincere, tranne quella che ha
la donna di picche che, forzando la sua natura, dirà una bugia. Dopo aver guardato le
carte, gli otto amici pronunciano le seguenti frasi. Aldo: “Nessun marito giocherà in coppia con sua moglie.” Barbara: “Mio marito Aldo siede tra Dario e Ivano.” Claudio: “Io e Aldo non abbiamo né il re di picche, né quello di quadri.” Dario: “Mia moglie ha la regina di cuori, la moglie di Ivano quella di quadri.” Elena: “Mio marito Ivano è davanti a Dario, alla destra di Aldo.” Francesca: “Mio marito è a sinistra di Claudio.” Giulia: “Mio marito Dario è a sinistra di Aldo.” Ivano: “Io e Aldo abbiamo il re di cuori e quello di picche.” A questo punto non resta che scoprire quali sono le coppie nella vita, quali le coppie nel tennis e quale carta possiede ognuno. |
| ENIGMA 69 Elisa A.M. 4 aprile 2006 [soluzioni] |
Con otto cubetti di 1cm di lato costruire, se esiste, una figura che abbia la superficie esterna di 26 cm2. Ogni cubetto deve avere almeno una faccia in comune con gli altri cubetti. |
| ENIGMA 68 Michela E. 27 marzo 2006 [soluzioni] |
Forse vi ricorderete che io sono emiliana (sono
nata in provincia di Piacenza) e come tutte (o quasi) le donne emiliane sono appassionata
di cucina. Mi piace cucinare e proporre ai miei ospiti i vari piatti tipici della mia
zona, a cominciare dai primi...lasagne, tortellini, crespelle. Fatto sta che durante i
nostri pranzi in mensa mi è venuto spesso spontaneo commentare di fronte a un piatto poco
invitante: "Ah, io di sicuro lo saprei fare meglio!" E dillo oggi, e dillo
domani...ai miei amici Mauro e Valerio è venuta la curiosità di vedermi all'opera e
così mi hanno gentilmente invitata (costretta? forzata?) a organizzare una cena a casa di
Valerio in cui avrei cucinato le mie specialità solo per loro. E così l'8 marzo scorso
(festa della donna) mi sono recata dopo pranzo a casa di Valerio per cucinare. Ho fatto le
lasagne ma proprio dall'inizio, a partire dal soffritto del sugo!! L'unica cosa che mi
sono concessa è di comprare le sfoglie di pasta già pronte (fare la pasta fatta in casa
sarebbe stato veramente troppo lungo!) Ma per il resto ho fatto tutto da sola, nessuno dei
miei amici si è affrettato a darmi una mano! Non solo, quando verso sera, esasperata e
piena di farina ho chiesto ai miei amici almeno di darmi una mano a mettere un po' di
ordine..quelli si sono messi a giocare! Incredibile, vero? (e infatti chi ci crede???) Ma
vi posso assicurare che Mauro e Valerio hanno iniziato il seguente gioco. Hanno preso le sfoglie di pasta per le lasagne che avevo avanzato (ed erano rimaste in tutto ben 2006 sfoglie! Come recitava una nota pubblicità: "le nostre porzioni sono sempre molto generose"!), le hanno disposte sul tavolo e poi a turno i due amici dovevano togliere dal tavolo un numero di sfoglie a loro scelta, purché maggiore o uguale a uno, e minore o uguale alla metà del numero di sfoglie che in quel momento erano sul tavolo. Il giocatore che lasciava sul tavolo una sola sfoglia perdeva. Ovviamente Mauro ha iniziato per primo a giocare (non sia mai detto che lasci a Valerio questo privilegio). A voi chiedo: determinare per quale dei due giocatori esiste una strategia vincente e descrivere tale strategia. P.S. La cena è stata un successo, ho ricevuto ben due proposte di matrimonio!!! Però, passare così la festa della donna... |
| ENIGMA 67 Anita P. 20 marzo 2006 [soluzioni] |
Ci sono 4 soldati che dopo una battaglia
disastrosa stanno battendo in ritirata. Per scappare al nemico devono attraversare un
ponte ma: il ponte può reggere soltanto due persone per volta, è buio, e dato che il
ponte è malridotto serve una torcia elettrica per attraversarlo, ma naturalmente i 4
soldati ne hanno una sola. I soldati dopo la battaglia sono in differenti condizioni
fisiche, quindi il soldato A ci mette un minuto a fare un attraversamento del ponte, il B
ce ne mette 2, il C ce ne mette 5 ed il D ce ne mette 10. È chiaro che quando due
militari attraversano il ponte insieme con la torcia, gli stessi procederanno alla
velocità del più lento dei due. Tanto per fargliela facile, i nostri 4 eroi hanno solo
17 minuti a disposizione per trovarsi tutti e 4 dalla parte opposta del ponte. E allora... come possono fare a tornare al campo base sani e salvi? |
| ENIGMA 66 Paolo C. 13 marzo 2006 [soluzioni] |
È possibile (e se si dire come, magari con un
disegnino) disporre 5 monete in modo che ugnuna di esse sia a contatto con tutte le altre? Si considerino le monete rotonde e tutte uguali. [Per i più pignoli: la soluzione che ho in mente funziona sia nel caso ideale di 5 circonferenze, ma anche nel caso di cilindri a patto che l'altezza del cilindro sia piccola rispetto al diametro... adesso non saprei quantificare, ma direi che l'altezza dovrebbe essere meno di un decimo del diametro, o giù di lì... più o meno come nel caso delle monete reali. Direi che le monete da 1 euro possono essere un buon modello per provare... Il fatto che le monete reali abbiano gli spigoli un po' arrotondati è influente.] |
| ENIGMA 65 Stefano P. 20 febbraio 2006 [soluzioni] |
Forse ricorderete nella cronaca nera più
recente il famoso caso del serial killer delle lampadine. no? Beh, permettetevi di
aggiornarvi (provando a rivelarvi qualche retroscena), anche perché in un certo senso
siamo responsabili anche noi di quanto é accaduto... Intanto vi ricordate del nostro piccolo Gigetto? Beh, tanto piccolo non lo è più, infatti ormai è cresciuto ed è diventato un uomo (lo so che l'abbiamo lasciato bambino meno di un anno fa, ma nel mirabolante mondo degli enigmi anche queste cose accadono, quindi non stupitevi troppo). Purtroppo la sua infanzia trascorsa tra giochi matematici e non, tra inverosimili piramidi di tupperware e genitori altrettanto malati di lui non poteva non lasciare il segno... pensate che disastrose conseguenze possono avere tutte queste cose sulla fragile mente di un bambino che sta formandosi giorno dopo giorno... e in effetti il trauma di essere cresciuto in una famiglia come la sua e di aver usato e abusato dei piaceri dell'enigmistica fin dalla più tenera età, beh... hanno purtroppo provocato in lui degli scompensi terribili (del resto le prime avvisaglie di questi traumi sono chiaramente identificabili anche tra di noi... :-)). Comunque la faccenda è questa. Crescendo il (piccolo) Gigetto comincia a nutrire un lieve risentimento nei confronti di tutte le persone che nella vita preferiscono una vita di successo e realizzazione e disdegnano i piaceri dell'enigmistica perché li trovano inutili, improduttivi e buoni solo per sprecare tempo. Col tempo questo risentimento cresce fino a diventare una vera antipatia, poi una intolleanza ed infine un vero e proprio odio... finche decide di investirsi del ruolo di giustiziere per riportare le cose alla "normalità". Sarà certamente un caso, ma a partire da quel giorno cominciano una serie di efferati omicidi, che vengono battezzati dai giornali come gli omicidi del "killer delle lampadine". Infatti pare che tale serial killer (di cui non facciamo nomi... ma cosa aspettarsi dopo un'infanzia come la sua? ;-)) scelga la sua vittima, ma prima di ucciderla gli lascia ancora una possibilità di salvarsi, infatti la sottopone ad un piccolo gioco e la giustizia solo se non riesce a verirne a capo (nel giro di una settimana?). Il gioco è' il seguente. Su una console ci sono tre interrutori che comandano 100 lampadine disposte una accanto all'altra a formare una fila e numerate da 1 a 100. I tre interrutori hanno questo effetto sulle lampadine: 1 interrutore) Accende tutte quelle che sono spente e spegne tutte quelle accese (ovvero cambia "stato" a tutte e cento le lamapdine) 2 interrutore) cambia lo stato a tutte le lampadine dispari 3 interrutore) cambia stato a tutte le lampadine il cui numero è un multiplo di 3 aumentato di 1 All'inizio Giget... ehm... il killer delle lampadine mostra alla sua potenziale vittima le 100 lampadine, facendo osservare che sono tutte accese, poi le nasconde con un telo e per 1000 volte, senza che la vittima possa vedere le sue operazioni sugli interrutori, preme gli interrutori secondo un preciso ordine, dopodiché mostra alla vittima le lampadine numero 95 e 96 permettendogli di vedere che sono spente e domanda "quante lampadine sono accese?" Per quanto è dato sapere nessuna delle persone sottoposte a questo gioco è riuscita a eludere la triste sorte che aspetta i fallimentari... voi sapreste sopravvivre? |
| ENIGMA 64 Sofia S. 13 febbraio 2006 [soluzioni] |
Sui quattro lati di un parallelogrammo ed
esternamente ad esso si costruiscono quattro quadrati. Che figura si ottiene congiungendo i centri di questi quattro quadrati? Giustificare la risposta. |
| ENIGMA 63 Luca B. 6 febbraio 2006 [soluzioni] |
La stella di Napoleone (enigma063.pdf) |
| ENIGMA 62 Sara D.M. 30 gennaio 2006 [soluzioni] |
Due
commercianti, Kostas e Nico, decidono di
andare al mercato per vendere delle galline prima gallina venduta, 1 euro; seconda gallina, 3 euro, terza gallina, 5 euro e così via A fine giornata, dopo aver venduto un certo numero di galline, dividono l´intero ricavato in mucchietti da 10 euro A turno ognuno di loro prende un mucchietto Kostas prende un mucchietto, Nico un altro mucchietto, poi Kostas prende un mucchietto, Nico un altro mucchietto e così via Alla fine però Kostas prende il penultimo mucchietto, contenente 10 euro, ma i due si accorgono che l´ultimo mucchietto rimasto, destinato a Nico, contiene meno di dieci euro Quanto costa il coltello? |
| ENIGMA 61 Simone B. 11 gennaio 2006 [soluzioni] |
Berlusconi, per confondere le idee ai
contribuenti e fregarli in un milione di modi diversi, ha deciso la seguente strategia per
la prossima finanziaria: le dichiarazioni dei redditi dovranno essere formulate scambiando
le cifre dei numeri con altri simboli scelti dal ministero. I simboli scelti per
quest'anno sono le lettere, e la chiave è data dalle relazioni seguenti: AB+AC=DE E+F=AB C+DF=GH (dove per AB si intende A decine e B unità e così via). Sapendo che I-J=1, riusciranno i nostri contribuenti a trovare la chiave e compilare la dichiarazione dei redditi? |
| ENIGMA 60 Giovanni V. 20 dicembre 2005 [soluzioni] |
Il buon vecchio Melchiorre aveva tre figli e morendo lasciò loro 17 cammelli. L'eredità andava divisa tra i figli in modo da assegnarne metà al primo, un terzo al secondo e un nono al terzo. I figli, non riuscendo a concludere la spartizione da soli, si rivolsero ad un giudice; questi grazie ad un espediente riuscì nell'impresa, rendendoli felici tutti e tre. Come? |
| ENIGMA 59 Luca L. 12 dicembre 2005 [soluzioni] |
In una piccola cittadina si trovano solamente due barbieri. Un turista decide di farsi tagliare i capelli. Uno dei due barbieri ha il negozio lindo e ordinato, specchi grandi e poltrone confortevoli; il barbiere stesso è ben tirato e ha i capelli ben tagliati e impomatati. L'altro ha una sala malmessa, con muri scrostati e poltrone traballanti, e ha i capelli mal tagliati, a formare una zazzera sbilena. In entrambi i saloni il prezzo è di 10 euro, ma il turista si dirige senza esitazione nel secondo. Per quale motivo? |
| ENIGMA 58 Silvia P. 5 dicembre 2005 [soluzioni] |
Siamo nella Valtrompia del futuro (chiedo scusa ai non valtrumplini se non riusciranno ad inquadrare la situazione, ma non è rilevante ai fini della risoluzione dell'enigma), dicevo, un futuro molto lontano perchè ci sarà addirittura la metropolitana. Un ragazzo abita a Sarezzo vicino alla stazione sotterranea. Gli piacciono due ragazze: una abita a Marcheno (quindi più a nord), l'altra a Concesio (più a sud). Dato che le due ragazze gli piacciono ugualmente e risiedono alla stessa distanza da casa sua, egli prende semplicemente il primo treno che passa, facendo decidere al caso da chi andare. I treni per le due direzioni passano con la stessa frequenza (ogni dieci minuti). Il giovanotto si reca alla fermata ogni sabato pomeriggio in un orario qualsiasi. Dopo un po', però, si accorge che passa più tempo con la ragazza di Concesio: infatti va da lei nove volte su dieci. Perché? |
| ENIGMA 57 Paolo P. 29 novembre 2005 [soluzioni] |
Il piccolo Gigetto è ancora alle prese con
delle scatole. Ne posside 3 di colori diversi. La sua mamma gli ha regalato delle palline
colorate, precisamente: 7 rosse, 4 blu, 5 verdi e 2 gialle. Ora il piccolo gigetto si
chiede in quanti modi diversi può disporre le palline nelle scatole. Ecco alcuni chiarimenti: 1. è possibile lasciare 1 o più scatole vuote. Ad esempio se metto tutte le palline in una scatola. 2. le scatole, essendo di colori diversi, sono da cosidearsi diverse. Ad esempio mettere tutte la palline nella prima scatola corrisponde a una configurazione diversa dal metterle tutte nella seconda. |
| ENIGMA 56 Fulvia S.R. 21 novembre 2005 [soluzioni] |
Alcune notti fa, mentre dormivo tranquillamente,
ho sognato un omino piccolo e strano: aveva in testa un cappello a punta e indosso un
lungo mantello blu, coperto di disegni, luminosi come stelle, che sembravano numeri.
Questo omino, dopo avermi osservato per un po', mi ha detto: "Sono il mago dei numeri e non credo che tu riesca a risolvere il mio enigma." Ho pensato: "Anche lui adesso mi propone degli enigmi!!! Non bastano gli amici della Sf.inge?" Ma lui, inesorabilmente, ha continuato: "Ogni numero intero positivo può venir scritto usando per tre volte la cifra 2 ed alcuni operatori matematici. Sei capace tu a trovare in che modo si possa fare ciò?" E poi è sparito senza dirmi niente di più. Ora, io ci sto pensando da quella notte e non dormo più! Se ci riuscite, mi dite come si fa e perché? Nota bene: la richiesta dell'enigma è di esprimere un qualsiasi numero intero positivo secondo una formula che prevede di scrivere esattamente per tre volte solo la cifra 2 e NON ALTRE CIFRE, insieme ad alcuni operatori matematici. |
| ENIGMA 55 Elisa A. M. 14 novembre 2005 [soluzioni] |
I punti che vedete in figura
sono disposti lungo una griglia ortogonale, cioè gli otto punti più esterni giacciono
sul perimetro di un quadrato, mentre il restante è al centro del quadrato stesso. Il
problema consiste nel coprire questi nove punti con quattro segmenti di retta senza mai
staccare la penna dal foglio. |
| ENIGMA 54 Michela E. 7 novembre 2005 [soluzioni] |
In un'isola ci sono due categorie di persone: i cavalieri, che dicono sempre la verità, e i furfanti, che mentono sempre. Un certo giorno si riunisce il gran consiglio, costituito da 2003 membri. Essi si siedono a caso intorno ad una tavola rotonda, e durante la riunione ciascuno di essi dichiara: "Entrambi i miei vicini sono furfanti." Il giorno dopo il consiglio si riunisce di nuovo, ma uno dei membri è malato, per cui sono presenti solo 2002 membri. Essi si ridispongono nuovamente a caso intorno alla tavola rotonda e ciascuno di essi dice: "Entrambi i miei vicini appartengono alla categoria opposta alla mia." Il malato era un furfante o un cavaliere? |
| ENIGMA 53 Stefano P. 31 ottobre 2005 [soluzioni] |
Vi ricordate di Gigetto (enigma 26)? Bene, una
cosa che non sapete di Gigetto è che vive in una famiglia piuttosto numerosa, almeno per
gli standard attuali. E ha anche un'altra caratteristica insolita: ha ben due fratelli
gemelli! Forse qualcuno di voi si è chiesto da dove deriva la passione per il calcolo e la genialità del fanciullo... la risposta probabilmente è racchiusa nei misteri della genetica e balza all'occhio immediatamente se mi permettete di raccontarvi come ha risposto suo padre Gigi quando Pino, il padre del suo grande amico Pinuccio (enigma 44) gli ha chiesto l'età. Gigi: "Beh... quanti anni ho... posso dirti che sommando il quadrato della mia età con i quadrati delle età dei miei figli e il quadrato dell'età di tuo figlio Pinuccio (che come sai è più grande di Gigetto), e poi aggiungendo 1 si ottiene 1998. Tieni conto che io regalo a Gigetto e ai suoi due fratelli 4 contenitori della Tupperware® a testa ad ogni compleanno, mentre so che tu regali a Pinuccio 14 pacchetti di biscotti ad ogni compleanno. Sapendo questo posso anche dirti che il quadrato della mia età, aumentato del numero di biscotti di Pinuccio e del numero di Tupperware® dei miei figli, e ancora incrementato di uno è uguale al prodotto delle età di mia moglie e mia madre che vive con noi e che hanno rispettivamente 29 e 71 anni... e questo dovrebbe bastarti!" Sapendo che Gigi ha tre soli figli gemelli, quanti anni ha Gigi? |
| ENIGMA 52 Anita P. 17 ottobre 2005 [soluzioni] |
In una stanza ci sono 5 persone (voi non siete in questa stanza, ma potete vederle, sentirle e parlare con loro) che si mettono d'accordo nel seguente modo: uno di loro dice sempre la verità, mentre gli altri quattro rispondono alternativamente il vero e il falso ad ogni domanda (nel senso che se uno risponde il vero alla prima domanda, lo stesso risponderà il falso alla seconda domanda). Non solo non sapete chi dice il vero, ma non sapete neanche se un certo "quasi mentitore" comincia con il vero o con il falso. Dovete determinare chi è il veriterio. Potete fare due domande a chi volete (ad una stessa persona o a 2 diverse) di qualsiasi tipo (NON necessariamente che richiedano risposte sì / no). Che domande fate? |
| ENIGMA 51 Paolo C. 10 ottobre 2005 [soluzioni] |
Siamo nel califfato di Neplon agli inizi intorno
all'anno 1307, Mebdulas è prigioniero del perfido califfo Cliffino che lo tiene
prigioniero in quanto invidioso della sua bellezza. Come avete intuito, Cliffino è un
figuro oltremodo superbo, ed anche certo della sua superiorità nel campo della logica
matematica. Come in ogni soria che si rispetti, al nostro eroe viene data una possibilità
di liberazione, nel caso egli sappia risolvere l'enigma che il califfo gli propone. Cliffino: Mio caro Meb, nella mia infinita magnanimità ho deciso di darti una possibilità di salvezza... Meb [pensato]: Quanto sei sfigato! Cliffino: ... ti prometto la libertà se saprai risolvere l'enigma leggendario ... Meb [pensato]: ...ma quale enigma leggendario, come minimo lo hai letto su Donna Moderna! Cliffino: Caro Mebdulas, devi semplicemente indovinare il numero al quale sto pensando... Meb: semplice... ce ne sono iusto giusto un'infinità o forse più... Cliffino: Lascia mi finire, testa di Pauera! Il numero al quale sto pensando è un numero Naturale... Meb [pensato]: già meglio, ma dovrò fare ricorso al mio proverbiale intuito... Cliffino: ...compreso nell'intervallo chiuso [1,3]... Meb [pensato]: ah, praticamnte ho tre possibilità: 1,2,3. Non male! Cliffino: ...per indovinare il numero xhe sto pensando, potrai farmi una ed una sola domanda... Meb [pensato]: BEh, ha sto punto gli chiedo che numero è e taglio la testa al toro... Cliffino: ...ma la domanda che mi porrai dovra essere una domanda che ammetta come risposta soltano, "Sì", "No" oppure "Non lo so". Meb: mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm Come era immaginabile alla fine Mebdulal viene liberato con grande sorpresa e disappunto del perfido Cliffino... L'enigma della settimana è: Quale domanda ha posto Mebdulas a Califfino per poter scoprire il numero che nella mente di Califfino si celava? Naturalmente il tutto postulato che Cliffino per quanto perfido e superbo è sincero e conosce la matematica. Tenete poi presente che la soluzione c'è ma non è unica... direi che che ne sono una mezza infinità... per cui potete dare sfogo alla vostra fantasia. Saranno particolarmente apprezzate le soluzioni eleganti... si sa, anche l'occhio vuole la sua parte... |
| ENIGMA 50 Sara D.M. 11 luglio 2005 [soluzioni] |
Una piantagione di banane è situata in pieno
deserto. Il proprietario ha raccolto 3000 banane che vuole trasportare, con l'unico
cammello che ha a disposizione, fino al mercato più vicino che dista 1000 chilometri
dalla piantagione. Il cammello riesce a trasportare al massimo 1000 banane per volta e
mangia una banana per ogni chilometro percorso. Qual è il numero massimo di banane che l'uomo potrà vendere al mercato? |
| ENIGMA 49 Mauro A. 27 giugno 2005 [soluzioni] |
Ci sono due coccinelle maschio (A e C) e due
coccinelle femmina (B e D) poste ai vertici di un quadrato. Le coccinelle maschio si muovono verso le coccinelle femmina e le coccinelle femmina cercano di raggiungere i maschi: cioé coccinella A va verso B, B va verso C, C va verso D e D vuole prendere A. Così muovendosi percorrono una curva che li porterà ad incontrarsi al centro del quadrato. Quanta strada farà ogni coccinella tenendo conto che il lato del quadrato è 1 metro? |
| ENIGMA 48 Simone B. 20 giugno 2005 [soluzioni] |
Siamo ad un torneo di calcio
giovanile, e vi partecipano sei squadre: Juventus, Torino, Milan, Inter, Sampdoria e
Genoa. Si usa la formula a girone, quindi il calendario si svolge in cinque giornate, e si assegnano 3 punti per la vittoria, 1 per il pareggio e nessuno per la sconfitta. Il calendario è stabilito giornata per giornata come segue: 1 giornata: Juve-Inter Milan-Samp Torino-Genoa 2 giornata: Inter-Torino Juve-Milan Samp-Genoa 3 giornata: Torino-Milan Juve-Samp Inter-Genoa 4 giornata: Samp-Inter Milan-Genoa Torino-Juve 5 giornata: Juve-Genoa Milan-Inter Torino-Samp Sapendo che io sono juventino, e che quindi il Torino DEVE andare in B, la classifica finale è: Juventus 9 Genoa 7 Sampdoria 7 Inter 5 Milan 5 Torino 3 Sapendo in più che l'Inter, da scarsona com'è, non vince il derby, mentre la Juve (da juventino come sono) sì, si riesce a risalire a tutti i risultati delle partite? (risultati in forma 1x2 chiaramente...) |
| ENIGMA 47 Giovanni V. 15 giugno 2005 [soluzioni] |
Ordunque ecco i fatti: una notte mio zio stava leggendo a letto un libro prima di addormentarsi, ma la lettura era così coinvolgente che non si decideva a interrompere. A un certo punto sua moglie, che voleva dormire, spense la luce. La camera a quel punto era scura come il carbone però mio zio continuò a leggere tranquillamente. Come è possibile ciò? |
| ENIGMA 46 Luca L. 7 giugno 2005 [soluzioni] |
Supponiamo di essere ad un gioco di premi e di dover scegliere quale porta aprire fra le proposte del presentatore. Dietro una di queste c'è un'auto, nelle altre due... una capra. Noi scegliamo una porta, e come capita in tutte le puntate, il presentatore cio dice "Ne sei proprio sicuro? Puoi ancora cambiare la scelta: anzi, ti voglio aiutare" e apre una delle porte che non abbiamo scelto, mostrando una capra. Amesso che il nostro scopo sia quello di vincere l'auto, ci conviene cambiare scelta, o la cosa è indifferente? |
| ENIGMA 45 Silvia P. 30 maggio 2005 [soluzioni] |
Il nonno di Heidi acquista un terreno adibito a pascolo nel quale l'erba, che è già ad una certa altezza, cresce con ritmo costante. Il nonno ha una mucca, una capra e una pecora, e sa che ogni giorno la mucca mangia lo stesso quantitativo d'erba che viene mangiato insieme dalla capra e dalla pecora. Ha inoltre calcolato che, a partire dall'indomani, il pascolo sarebbe sufficiente a nutrire la mucca e la capra per 45 giorni fino a sera, oppure la mucca e la pecora per 60 giorni, oppure la capra e la pecora per 90 giorni. In tutti e tre i casi, alla fine non resterebbe più un filo d'erba.Per quanti giorni nutrirebbe la mucca, la capra e la pecora contemporaneamente? |
| ENIGMA 44 Paolo P. 23 maggio 2005 [soluzioni] |
Il piccolo Pinuccio (amico di Gigetto, vedi
enigma 26) è anche lui un bambino molto creativo e gioca con 11 contenitori di colori
diversi che la mamma gli ha regalato. Ad un certo punto gli viene fame, va in cucina e
trova in un barattolo la bellezza di 27 biscotti! Pinuccio è un golosone ed è molto
contento della scoperta, ma essendo anche un bambino accorto, ne mangia solo 4 e vuole
mettere i restanti 23 nei contenitori, e conservarli per i giorni successivi. Si accorge
poi, che in ogni contenitore ci stanno al massimo 4 biscotti. Allora Pinuccio si
chiede: in quanti modi posso disporre i 23 biscotti negli 11 diversi contenitori con il
vincolo di non poter mettere più di 4 biscotti per contenitore? Attenzione: * I contenitori sono diversi, perché hanno diversi colori, per esempio: 2 in quello rosso e 1 in quello verde e diverso da 2 in verde e 1 in rosso o (2,1) non è uguale a (1,2) * In ogni contenitore non necessariamente ci devo mettere un biscotto, non ho posto questo vincolo, se il problema lo consente alcuni possono rimanere anche vuoti. |
| ENIGMA 43 Fulvia S.R. 17 maggio 2005 [soluzioni] |
Durante un weekend di primavera Lorenzo, che ama
videoregistrare un sacco di programmi in televisione, si trova a dover risolvere un
problema. Guardando il giornale, si è accorto infatti che quella notte dall'1,45 alle
3,15 sarà trasmesso un programma a cui tiene molto. Ora, Lorenzo è rimasto senza
videocassette VHS vuote, non vuole coprire programmi già registrati su altre
videocassette, i negozi sono già chiusi, non ha nessuno a cui chiedere una videocassetta
in prestito e quella sera, dovendo uscire, tornerà molto tardi e perderà sicuramente il
programma. Dopo aver cercato tra le videocassette se ce n'è una con un po' di spazio
libero, ne trova solo una utilizzabile che ha appena mezz'ora disponibile. Lorenzo ci
pensa un po' su e poi dice: "Ma certo!" e riesce a registrare su quella cassetta
tutto il programma, che inizia e termina secondo gli orari segnalati. Il suo è un normale videoregistratore, con cui non è possibile registrare su "hard disk". Come ha risolto il problema? |
| ENIGMA 42 Elisa A.M. 9 maggio 2005 [soluzioni] |
Siamo nel mondo dei leggendari cavalieri della
tavola rotonda, a Camelot. Sir Lancillotto deve partire per una missione di durata massima
di un mese (30 giorni) su ordine di Artù (sono solo scuse per tenerlo lontano da
Ginevra... ). Purtroppo, il nobile destriero di Lancillotto si è azzoppato rincorrendo la
puledrina di Ginevra, così Lancillotto è costretto a chiedere in prestito un cavallo
alla scuderia di Artù. Anche nel mondo fantastico di Camelot, purtroppo, nessuno dà
niente per niente... Artù desidera qualcosa in cambio. Ora, Lancillotto possiede una catena d'oro composta da trenta anelli e non richiusa su se stessa. Artù chiede a Lancillotto un anello di questa catena per ogni giorno in cui Lancillotto utilizzerà il destriero che Artù gli presta. Merlino, eletto arbitro della situazione, sarebbe il depositario della catena fino al ritorno del cavaliere e avrebbe il compito, ogni giorno di assenza di Lancillotto, di pagare in modo adeguato Artù utilizzando gli anelli della catena. Lancillotto, che era un gran bel pezzo di cavaliere, ma non proprio un'aquila, si lamenta con Merlino perchè non vuole che la sua catena ogni sia spezzata in corrispondenza di ogni anello. Egli confida infatti di riuscire a tornare prima dei trenta giorni richiesti da Artù. Inoltre, l'eventuale "riaggancio" degli anelli costerebbe una cifra dal fabbro di Camelot! Merlino lo rassicura: esiste un numero minimo, ben inferiore a 29, di anelli da spezzare per coprire i pagamenti di ogni giorno della sua assenza. Qual è il numero minimo di anelli della catena che occorre rompere perchè questo sia possibile? Per capirci meglio, immaginiamoci cosa accade: Il primo giorno in cui Lancillotto non ha fatto ritorno, Artù si presenta da Merlino e chiede il pagamento e Merlino deve dargli un anello. Il secondo giorno in cui Lancillotto non fa ritorno, stessa scena: Merlino deve dare ad Artù due anelli. Il terzo giorno idem, e così via... Facciamo fino al 20mo giorno in cui Lancillotto non fa ritorno. Artù va da Merlino e chiede il pagamento per 20 anelli (staccati, attaccati, ad Artù poco interessa). Il 21mo giorno Lancillotto torna. Ora, se Merlino non fosse intelligente, dovrebbe ogni giorno staccare un anello dalla catena. Ma, dato che è intelligente, ha trovato un modo per ottenere tutte le combinazioni possibili di quantità di anelli (dal minimo di 1 ad un massimo di 30) rompendo (volendo anche a priori, senza sapere quando tornerà Lancillotto) la catena in pochi punti strategici. |
| ENIGMA 41 Michela E. 2 maggio 2005 [soluzioni] |
Michela e Stefano ogni giorno si fanno
avvelenare...ehm...decidono di pranzare insieme alla mensa della facoltà'. La mensa è
frequentata da molti studenti per cui spesso le code sono piuttosto lunghe. A volte quindi
i due amici, onde evitare di lasciare che Michela chiacchieri per tutto il tempo della
coda, decidono di ingannare il tempo giocando al seguente gioco, per il quale coinvolgono
anche il loro amico Cesare anche lui in coda (che anche lui si lascia coinvolgere
volentieri pur di non lasciare chiacchierare Michela oltre misura!). Il gioco funziona
così: Cesare estrae dal proprio portafogli alcune monete, le divide in due pile e tiene nella mano destra una pila di m monete e nella mano sinistra una pila di n monete. Michela e Stefano possono scegliere a turno una delle seguenti mosse: - prendere una moneta da una delle due pile; - prendere una moneta da ciascuna delle due pile; - spostare una moneta da una pila all'altra. Perde chi non può più muovere. Comincia Michela (perché Stefano è cavaliere). Determinare in funzione dei numeri n ed m se uno dei due giocatori ha una strategia vincente e in caso affermativo specificare di quale giocatore si tratta. (alla fine del gioco tutte le monete vengono restituite a Cesare che altrimenti digiuna! :-)) |
| ENIGMA 40 Anita P. 25 aprile 2005 [soluzioni] |
Scrivere i numeri da 1 a 9 all'interno delle parti di piano comprese tra i cinque cerchi olimpici, in modo che la somma dei numeri scritti all'interno di ciascun cerchio sia costante. |
| ENIGMA 39 Paolo C. 18 aprile 2005 [soluzioni] |
Ho comprato un libro un po' particolare:
l'epilogo è prima del prologo, l'introduzione è dopo l'indice e la fine è nella prima
metà del libro. Di che libro si tratta? |
| ENIGMA 38 Stefano P. 11 aprile 2005 [soluzioni] |
La cagnetta Twiggy ama le noci, ma non riesce a
romperle, allora deve portarle al suo padrone affinché lui faccia questa operazione al
suo posto. Tra il padrone e l'animale la regola del gioco è relativamente semplice. Il padrone divide tutte le noci che Twiggy gli ha portato in due mucchietti uguali e ne mette da parte uno. Se così facendo resta una noce, questa è per Twiggy. Poi ripete l'operazione fino all'esaurimento delle noci. Per esempio, se Twiggy porta 1903 noci, i mucchietti successivi saranno di 951, 475, 237, 118, 59, 29, 14, 7, 3 e 1 noci e Twiggy avrà potuto mangiare 9 noci. Twiggy può portare al padrone al massimo 1998 noci e ne porta sempre almeno 1798. Quante noci deve portare al minimo Twiggy per poterne mangiare il più possibile? |
| ENIGMA 37 Fulvia S.R. 4 aprile 2005 [soluzioni] |
In una casa ci sono 4 stanze che contengono
ciascuna una palla, un tavolo ed una sedia, che sono colorati di blu, giallo, rosso o
verde. Ogni palla ha un colore diverso rispetto alle altre e così pure ogni tavolo e ogni
sedia. In ogni stanza i tre oggetti potrebbero essere dello stesso colore, di due colori o
di tre colori diversi. Ho le seguenti informazioni: 1) La palla rossa è nella stanza con il tavolo del suo colore complementare, ma non con la sedia gialla. 2) La palla gialla è nella stanza con un tavolo non del suo colore complementare. 3) Due stanze hanno all'interno gli stessi tre colori. 4) Il tavolo giallo è nella stanza con la sedia rossa. 5) In una stanza la palla ha lo stesso colore della sedia, ma questo colore non è il verde. Inoltre, io so che una di queste informazioni è sicuramente inutile. Come sono disposti in base ai colori gli oggetti nelle 4 stanze e perché? |
| ENIGMA 36 Sofia S. 28 marzo 2005 [soluzioni] |
È più facile, ottenere 6 gettando una sola volta un dado, oppure gettandolo 3 volte ottenere tutte e tre le volte un numero pari (non necessariamente lo stesso)? |
| ENIGMA 35 Paolo P. 21 marzo 2005 [soluzioni] |
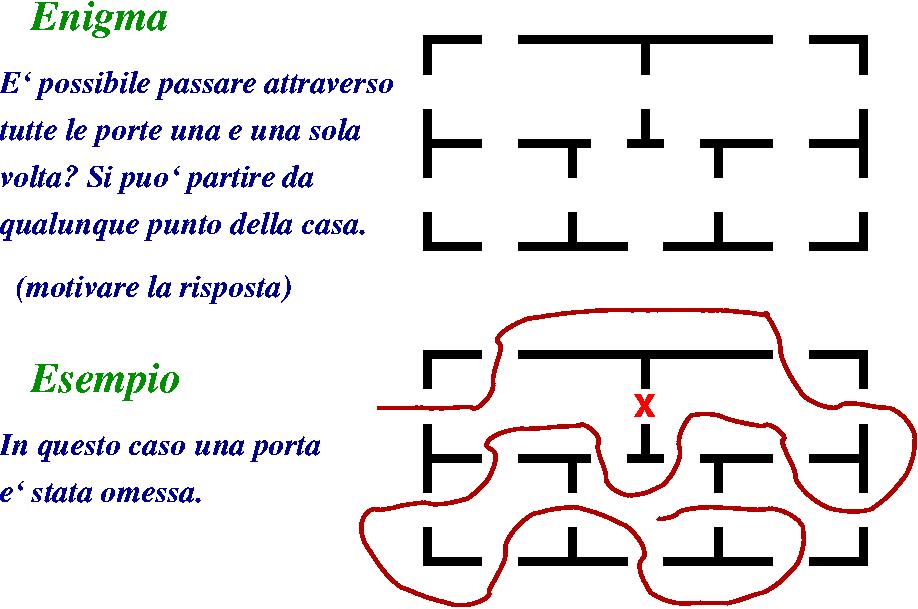 |
| ENIGMA 34 Luca L. 14 marzo 2005 [soluzioni] |
Uno schema tipo battaglia navale è costituito da 19 linee orizzontali e 98 colonne. Antonio ha scritto le 26 lettere dell'alfabeto in ordine, riga per riga, una lettera per casella, cominciando dalla lettera A nella casella (1,1), e ripetendo l'alfabeto tante volte quante sono necessarie per arrivare all'ultima casella (19,98). Luca ha fatto la setssa cosa, ma lavorando sulle colonne, annerendo via via tutte le caselle in cui compaiono lettere uguali. Quante caselle ha dovuto annerire Luca? |
| ENIGMA 33 Silvia P. 7 marzo 2005 [soluzioni] |
I tre amici matematici Angelo
(omaggio dovuto a Francesco Renga), Bruno e Carlo si ritrovano dopo molti anni e si
scambiano informazioni sulle età dei loro figli. Bruno nota che il maggiore dei suoi tre
figli, che sono nati in tre anni consecutivi, ha il triplo degli anni del figlio di Carlo.
Angelo constata che, se Bruno sommasse le età dei suoi tre figli e poi sommasse le
cifre del risultato tra di loro fino ad ottenere una sola cifra, otterrebbe l'età della
figlia di Angelo stesso, che ha due anni in meno della figlia di Carlo. Quanti anni hanno i tre figli di Bruno? |
| ENIGMA 32 Giovanni V. 3 marzo 2005 [soluzioni] |
Vedete in quante fogge mi tramuto prima son maschio e vivo sotterrato; di nuovo nasco e in femmina mi muto, poi tagliato a traverso e bastonato maschio ritorno, e quindi ancor premuto e fatto in polpe, in femina cangiato mi trovo, e annegato, e messo al foco, ritorno maschio, e cangio abito e loco. |
| ENIGMA 31 Luca N. 21 febbraio 2005 [soluzioni] |
Un pirata cattura un capitano e gli dice:
"Se mi dici una verità ti impicco, se mi dici una bugia ti fucilo". Il capitano
allora pronuncia una affermazione di senso compiuto (non una domanda, ma una
affermazione...) ed il pirata è costretto a lasciarlo andare. Qual è la frase che pronuncia il capitano? |
| ENIGMA 30 Elisa A.M. 14 febbraio 2005 [soluzioni] |
Ci sono tre scatoloni; il primo contiene due
palline bianche, il secondo due palline nere ed il terzo una bianca e una nera. Sui rispettivi coperchi ci sono le scritte BB, NN e BN ma i coperchi sono messi in disordine in modo tale che quello che c’è scritto sul coperchio sicuramente non coincide con quanto contenuto all’interno dello scatolone. Quante palline è necessario estrarre, al minimo, per determinare l’esatto contenuto dei tre scatoloni? |
| ENIGMA 29 Michela E. 7 febbraio 2005 [soluzioni] |
Quattro amici che non si vedevano da tempo si
ritrovano a una festa di carnevale vestiti tutti e quattro da pirati. Cominciano a
chiacchierare del più e del meno (come dei bravi matematici!) finché il discorso si
sposta sui figli. Allora il primo "pirata" dice: - Ciascuno di noi ha un figlio! - Esatto - replica il secondo - ma i vostri tre figli hanno tutti la stessa età, contrariamente al mio! - Pensate che tutti insieme hanno esattamente 50 anni! - sottolinea il terzo. Il quarto allora nota: - Come passa il tempo! 10 anni fa la somma delle età dei nostri figli era solo di 12 anni! Dopo questa nota sul tempo che fugge i 4 si buttano su un piatto di ottime frittelle!!! E a voi, non rimane la curiosità di sapere qual è l'età attuale del figlio del secondo "pirata"? |
| ENIGMA 28 Anita P. 1 febbraio 2005 [soluzioni] |
Due persone compiono gli anni lo stesso giorno, ma hanno età differenti. Per sei compleanni consecutivi l'età di una è un multiplo esatto dell'età dell'altra. Quanti anni compiono i due al sesto di questi compleanni? |
| ENIGMA 27 Paolo C. 24 gennaio 2005 [soluzioni] |
In un paese tutti gli abitanti sono ladri. Non
si può camminare per strada con degli oggetti, senza che vengano rubati e l'unico modo
per spedire qualcosa senza che venga rubato dai postini è di rinchiuderlo in una
cassaforte chiusa con un lucchetto. Ovunque l'unica cosa che non viene rubata è una
cassaforte chiusa con un lucchetto, mentre sia le casseforti aperte, sia i lucchetti
vengono rubati. Alla nascita ogni abitante riceve una cassaforte ed un lucchetto di cui
possiede l'unica copia della chiave. Ogni cassaforte può essere chiusa anche con più
lucchetti ma la chiave non è cedibile e non può essere portata fuori dalla casa del
proprietario, perché verrebbe rubata durante il trasporto. Non si può in alcun modo fare
una copia delle chiavi. Come può un abitante di questo paese spedire il regalo di compleanno ad un proprio amico? |
| ENIGMA 26 Stefano P. 11 gennaio 2005 [soluzioni] |
Il piccolo Gigetto è un bambino molto creativo,
uno che, per la gioia del portafoglio dei suoi genitori, riesce a divertirsi con poco e
passa ore a giocare con i piccoli oggetti della vita quotidiana che trova in casa. Oggi,
in particolare, ha trovato in un armadietto della cucina, i 13 contenitori della
Tupperware® della mamma (per chi non sapesse che cosa sono: semplicemente dei contenitori
in plastica di diverse dimensioni che si possono inscatolare uno dentro l'altro) e subito
si è ingegnato per trovare un modo divertente di giocarci. La sua idea è stata questa:
dopo aver osservato che tutti e 13 i contenitori hanno dimensioni diverse, ne sceglie uno
qualsiasi che non sia, però, il più grande. Quindi inserisce il contenitore scelto
dentro uno qualsiasi degli altri (ovviamente lo deve inserire dentro uno di quelli più
grandi, altrimenti non può farcelo entrare!), e procede così, inserendo i due
contenitori già inscatolati dentro un terzo più grande, e così via fino ad
inserire la sua matrioska dentro il contenitore più grande di tutti; a questo punto il
gioco è finito. Ovviamente al termine del gioco non tutti i contenitori sono stati
utilizzati ed inscatolati uno dentro l'altro: alcuni possono essere stati saltati nella
procedura, ma questo non è un problema. Ben presto, nonostante la fantasia e la
creatività che lo contraddistinguono, il piccolo Gigetto comincia ad annoiarsi a giocare
in questo modo, e, visto che oltre alle succitate qualità il frugoletto dispone di una
curiosità ed una sagacia notevoli, decide di provare a scoprire in quanti modi diversi è
possibile giocare il suo gioco, ovvero in quanti modi diversi si possono inscatolare i 13
tupperware della mamma mai partendo dal più grande ma terminando sempre con il più
grande. Questa nuova sfida lo impegna per un'oretta circa, ma alla fine, visto che oltre
alle succitate qualità il piccolo dispone anche di una notevole intelligenza, produce la
sua risposta e corre orgoglioso a raccontare alla mamma come ha fatto... Voi volete essere da meno? :-) |
| ENIGMA 25 Paolo P. 29 dicembre 2004 [soluzioni] |
Prendiamo un sfera di raggio R, facciamo un buco con un trapano che passa per il centro, in questo modo abbiamo rimosso le due calotte e un cilindro ottenendo un anello. Ora misuriamo l'altezza L di questo anello, se si calcola li volume di questo solido si noterà che questo non dipende da R ma solo da L. |
| ENIGMA 24 Luca L. 13 dicembre 2004 [soluzioni] |
Siamo a Granada, in Spagna, dove un'avvenente
guida turistica di nome Salomè sta accompagnando un gruppo di giovani matematici in
visita all'Alhambra, antica città circondata da mura e ricca di giardini e templi. Giusto
per capire la profondità delle spiegazioni di Salomè, vediamo un esempio: "This is
a very romantic river, and it has the same name of the city, because the city has the same
name of the river". Arriviamo al primo tempio da visitare, con la pavimentazione di forma rettangolare, e non quadrata, ricoperto da mattonelle quadrate da 50 cm di lato. Le mattonelle sono di due colori diversi, gialle e rosse. Quelle gialle ricoprono un rettangolo centrale. Le mattonelle rosse coprono invece una bordura di larghezza costante attorno al rettangolo giallo. Le mattonelle gialle e quelle rosse sono in numero diverso; nonostante ciò, Salomè fa osservare che è possibile, utilizzando le stesse mattonelle del pavimento, mettere le rosse a formare un rettangolo centrale, e le gialle a formare la bordura. Quanto vale, COME MINIMO, la misura della superficie del pavimento del tempio? |
| ENIGMA 23 Silvia P. 6 dicembre 2004 [soluzioni] |
Dovete trovare il successivo a
questa serie di numeri: 1 11 21 1211 111221 312211 Anche in questo caso, come nell'enigma 22, non dovete affidarvi troppo ad un matematico... |
| ENIGMA 22 Giovanni V. 29 novembre 2004 [soluzioni] |
Per questa settimana l'enigma è qualcosa che
viene attribuito al buonvecchio Galileo. Il grande pisano, per tenere alla larga i visitatori che lo assillavano in continuazione, diede a un domestico l'ordine di stare di guardia alla porta... con foglio e calamaio. Sul foglio c'era un quesito che il servo avrebbe dovuto sottoporre a chi avesse voluto incontrarlo. Il visitatore avrebbe quindi scritto sul foglio la sua risposta e il motivo della visita, che il servo sarebbe andato a consegnare a Galileo. A questo punto, se la porta non si fosse aperta dopo due o tre minuti, il visitatore avrebbe dovuto andarsene. Il problema era trovare il successivo di questa serie di numeri (o comunque di spiegarne l'ordinamento): 5 10 2 9 8 4 6 7 3 1. Il testo consigliava di capire l'ordine logico ma di non affidarsi ad un matematico perché la soluzione ... non sta nei numeri. [Suggerimento: se l'enigma fosse di Newton la sequenza sarebbe quasi certamente diversa, e così se fosse di Heisenberg. Inoltre quasi certamente anche le loro due sequenze sarebbero tra loro diverse. Se invece l'enigma fosse di Tartaglia, sarebbe identico a quello di Galileo.] |
| ENIGMA 21 Luca N. 22 novembre 2004 [soluzioni] |
Il famoso investigatore Sherlock Holmes muore e
il suo spirito si trova quindi al cospetto di San Pietro per il giudizio. Tuttavia
quest'ultimo è molto impegnato nelle riprese del suo ultimo spot per la Lavazza e decide
di non perdere troppo tempo con lui. Conoscendo la proverbiale perspicacia dello spirito
defunto, lo scaraventa in una stanza nella quale ci sono solo due porte identiche e gli
spiega in fretta e furia: "Caro Sherlock, una di queste porte ti condurrà in
Paradiso, l'altra all'Inferno. Come vedi davanti a ciascuna porta vi è un angelo: sappi
che uno dei due dice sempre e solo bugie, l'altro dice sempre e solo la verità e non è
detto che davanti alla porta dell' inferno ci sia l'angelo bugiardo e davanti alla porta
del Paradiso ci sia l'angelo sincero. Puoi fare una sola domanda ad uno solo dei due angeli per capire qual è la porta per il Paradiso. Buona fortuna..." e scappa via chiamato da Bonolis... L'investigatore riflette qualche secondo, deciso a risolvere anche quest'ultimo caso, dopodiché esclama "Elementare...!!!...", fa la sua domanda ad uno dei due angeli e attraversa sereno la porta per il Paradiso. Qual è questa domanda? Note: Sherlock Holmes non sa ovviamente quale dei due angeli sia il bugiardo (e quale il sincero) e come siano disposti rispetto alle due porte. |
| ENIGMA 20 Elisa A.M. 15 novembre 2004 [soluzioni] |
I tre porcellini si trovano alla reception
dell'hotel gestito da Nonna Papera per prendere una camera in cui trascorrere la notte,
dopo essere stati sfrattati dal lupo cattivo (nella realtà, il vecchio Ezechiele ha
buttato giù anche la casetta di mattoni, non con il solo fiato, ma aiutandosi con un
bulldozer... mica tont!). Nonna Papera assegna loro la camera 302, una carinissima tripla
fatta di pan-di-spagna e cioccolata, e i tre porcellini danno complessivamente 30 euro
alla Nonna. Dopo che i prosciuttini se ne vanno per raggiungere la loro stanza, Nonna
Papera si rende conto che il prezzo reale della stanza di pan-di-spagna non era di 30
euro, ma di 25 euro! Dispiaciutissima per l'inconveniente, la Nonna chiama Ciccio, il suo
aiutante, e gli consegna 5 euro in monete da 1 euro e gli chiede gentilmente di portarli
in resto ai tre salamini, insieme con le sue scuse. Mentre si reca verso la camera delle
tre porchette, Ciccio ragiona tra se' che sarebbe difficile dividere 5 euro tra tre
persone... 5:3=?... Insomma, avrebbe messo in difficoltà i tre insaccati... Così,
sfoderando uno dei suoi migliori sorrisetti furbetti, Ciccio si intasca 2 euro e consegna
1 euro a ciascun porcellino, porgendo le scuse di Nonna Papera. Riepilogando la situazione, ogni porcellino ha pagato 9 euro, per un totale di 27 euro. Ciccio si è intascato 2 euro, totale: 29 euro... Dove è finito il restante euro? ------ Ndr: In realtà, non è il vero Ciccio ad aver commesso il furtarello, bensì il Bassotto 167-671 travestito... Sia mai che un "buono" di Walt Disney sia tacciato di disonestà!!! Ndr(2): Si vede che ho fame...?? |
| ENIGMA 19 Michela E. 8 novembre 2004 [soluzioni] |
Dovete sapere che nell'isola dei famosi - non
sono un'appassionata di tale programma ma mi serve per la scenografia - vive una
popolazione di camaleonti. Questi simpatici animaletti sono capaci di assumere 3 colori
diversi, giallo, verde e nero. Ora, da quando sull'isola è approdata questa folla di vips
per la popolazione dei camaleonti è iniziato l'inferno: disturbati dalla confusione e
dalle telecamere essi hanno iniziato ad essere sempre più stressati finché adesso
succede il seguente strano fatto: ogni qual volta due camaleonti di colore diverso si
incontrano essi assumono il terzo colore. Prima che arrivasse la banda di DJ Francesco e
soci è stata mandata la Ventura a contare quanti camaleonti ci fossero sull'isola e di
quale colore essi fossero. La poverina ci ha messo un bel po' e ne è quasi uscita pazza -
è per quello che Bettarini si è stufato e stanno divorziando - ma alla fine ne ha
contati 13 gialli, 15 verdi e 17 neri. Ora io vi chiedo, è possibile che ad un certo momento possa sucedere che tutti i camaleonti abbiano lo stesso colore???? Siccome le stime della Ventura possono non essere corrette, provate anche a risolvere lo stesso mistero nel caso generale in cui ci siano sull'isola a camaleonti gialli, b verdi e c neri (a,b,c numeri naturali). |
| ENIGMA 18 Sofia S. 18 ottobre 2004 [soluzioni] |
Paolo e Francesca hanno tre figli. Dante, loro vecchio amico, li incontra e chiede informazioni sulle età della loro prole. In tutta risposta i due gli dicono che la somma delle età dei tre pargoli è uguale al loro prodotto. Al che Dante capisce che tra i tre non ci sono gemelli e che, forzatamente, essi hanno rispettivamente 1, 2 e 3 anni. Come può Dante essere tanto sicuro? |
| ENIGMA 17 Anita P. 11 ottobre 2004 [soluzioni] |
Dovete scrivere una relazione che dia come risultato 20, ad esempio 17+3=20, ma potete utilizzare solo le seguenti cifre: 0, 3, 3 (ossia: potete utilizzare la cifra 0 una e una sola volta e la cifra 3 due e due sole volte). È possibile usar tutte le operazioni che conoscete, ma non si possono usare incognite. |
| ENIGMA 16 Paolo C. 29 giugno 2004 [soluzioni] |
Ernestino Ising (http://www.bradley.edu/las/phy/personnel/ising.html),
detto Tino, è un giovane neolaureato in fisica. Il tema della sua ricerca lo coinvolge molto, tuttavia il suo spirito avventuriero lo spinge a compiere un viaggio nel cuore dell'africa (siamo nella metà degli anni '50). Decide così di imbarcarsi su una piccola canoa e risalire il corso del fiume Nilo. Il viaggio procede tranquillamente fino a quando a causa dell'aggressione da parte di un coccodrillo la sua canoa risulta danneggiata, ed è costretto ad approdare a riva in un territorio sconoscuito ed inesplorato. E' notte. E' così che viene fatto prigioniero dalla tribù dei Meani Feldani che avevano sentito i rumori del combattimento nel fiume. La sua prigione è assai singolare: egli si ritova al centro di un tracciato ettagonale l'intero villaggio fuori dal Sacro Ettagono lo guarda incuriosita, aspettandosi qualcosa di strano dall'insolito viaggiatore. Ai sette vertici della sua prigione Tino vede sette lampade accese. Egli è perfettamante libero "fisicamente" eppure è imprigionato: si ricorda infatti di aver letto delle antiche leggende sulle lampade "kuma" che in feldano significa lampada "collettiva-sacra". Egli potrà uscire dall'ettagono solamente quando tutte le lampade saranno spente, se dovesse uscire prima una potentissima maledizione si abbatterà sull'intero villaggio. Spegnere le lapade non è difficile, è sufficiente un soffio, ma la particolarità di queste lampade è che soffiando su una lampada accesa(soffiando su una lampada spanta non succede nulla) non solo quasta si spegne, ma si spengono anche le due lampade posizionate nei vertici vicini se sono accese, mentre si accendono, se sono spente. In breve, spegnendo una lampada, cambia anche lo stato delle due lampade adiacenti. La libertà è a portata di mano, deve solo spegnere tutte le lampade ed è libero, in più libererà il popolo meano dall'atroce maledizione, ma deve fare in fretta perchè manca poco tempo al sorgere del sole e con il giorno i meana lo uccideranno... Come può fare per spegnere le kuma nel minor numero di soffi possibile? |
| ENIGMA 15.3 Stefano P. 21 giugno 2004 [soluzioni] |
Clodoveo, il bisnonno di Guendalina, non e' ancora centenario ma ha un'età molto avanzata. Tutto ciò che posso dirvi e' che, l'anno scorso, la sua età era un multiplo di 8 e che l'anno prossimo sarà un multiplo di 7. Quanti anni ha nonno Clodoveo? |
| ENIGMA 15.2 Stefano P. 21 giugno 2004 [soluzioni] |
Due famiglie di formiche, la prima composta da 5 formiche rosse, la seconda da cinque formiche nere, decidono, come e' abitudine fare tra le brave formiche d'estate, di andarsene in vacanza. Per problemi economici non possono permettersi di affittare un formicaio in una località turistica, quindi decidono di comune accordo di scambiarsi i rispettivi formicai per trascorrere la villeggiatura "lontano" da casa, ma senza spendere troppo. Ogni formica porta con se' il suo bagaglio e ci mette 3 minuti e 30 secondi per raggiungere il formicaio dell'altra famiglia. La partenza delle prime formiche di ogni famiglia (quindi una rossa e una nera) avviene nello stesso momento per le due famiglie, poi ogni formica di ciascuna famiglia parte un minuto dopo la precedente. Poiche' esiste una sola strada che collega i due formicai, le formiche rosse e quelle nere si incrociano durante il loro cammino e, in questa occasione, ogni formica augura "Buone vacanze!" all'altra; le formiche non si scambiano mai frasi augurali all'interno del formicaio. Quanti "Buone vacanze!" saranno pronunciati durante il trasferimento? |
| ENIGMA 15.1 Stefano P. 21 giugno 2004 [soluzioni] |
Sei mariti e sei mogli partecipano ad un party. Alcuni degli invitati stringono la mano ad altri invitati, ma mai al proprio consorte. Uno di essi chiede a tutti gli altri quante strette di mano hanno ricevuto nel corso della serata, ottenendo unidici risposte diverse. Quante mani ha stretto sua moglie? |
| ENIGMA 14.2 Paolo P. 14 giugno 2004 [soluzioni] |
Un signore finisce di lavorare ad una certa ora prende il treno per arrivare a casa e alle 5 arriva alla stazione. Sua moglie parte da casa in macchina e guida sempre alla stessa velocita`, arriva esattamente alle 5 in stazione, in tempo nullo carica il marito e si gira, poi riparte alla solita velocita`. Un giorno il marito arriva in stazione alle 4 e si mette a camminare, ad un certo momento incontra la moglie e tornano assime a casa. Questa volta arrivano a casa mezz'ora prima del solito. La domanda e`: per quanto tempo ha camminato l'uomo? |
| ENIGMA 14.1 Paolo P. 14 giugno 2004 [soluzioni] |
Ho a disposizione 12 palline uguali. Arriva un infiltrato, entra nella stanza con in mano una pallina falsa e poi se ne esce. Puo` aver sostituito la pallina oppure no. Ho a disposizione una bilancia a bracci (quelle che danno l'equilibrio) e con tre pesate devo stabilire se l'infiltrato ha sostituito la pallina. Se la ha sostituita, devo dire se pesa di piu` o di meno. |
| ENIGMA 13.2 Diego G. 7 giugno 2004 [soluzioni] |
Quale parola del primo gruppo
appartengono anche al secondo, e perchè? Primo gruppo: BANCA - SPORCO - CARTE - TORSO Secondo gruppo: CANE - LEPRE - GATTO - TIGRE |
| ENIGMA 13.1 Diego G. 7 giugno 2004 [soluzioni] |
L'ispettore Lumière deve
risolvere l'ennesimo caso capitatogli nella piccola e ridente città di San Salvo a Mare. Il suo giovane luogotenete Srg. Panico allora inizia a introdurgli gli indiziati di quello che si prospetta come un raro caso di sequestro di persona. Un uomo un certo Nelson viene allora introdotto nel suo ufficio. Ha la barba non fatta, i vestiti strappati in corrispondenza delle ginocchia e ferite alle braccia e alla testa. "Sono vivo per miracolo" esordisce il malconcio soggetto. "Il mio socio Giulius, col quale sono in pessimi rapporti d'affari, ha cercato di farmi rapire, per poi probabilmente farmi fuori o costringermi a firmare la cessione della mia quota azionaria". Ma io, sono riuscito a liberarmi e a scappare". "Bene" dice Venturi "racconti come si sono svolti i fatti". "Uscivo dall'ufficio quando due tizi con il volto coperto da maschere delle tartarughe ninja mi hanno aggredito nel garage dell'azienda, mi hanno caricato e portato in una cascina diroccata e isolata dal resto del mondo. Al momento di entrare in casa, mentre trafficavano con la serratura hanno avuto un attimo di distrazione, così dato che la porta era stata lasciata aperta, l'ho tirata con forza verso di me facendola sbattere addosso ai due ceffi che si trovavano ancora sull'uscio. Ne è seguita una collutazione, nella quale come si vede ho avuto la peggio. Così i due mi hanno trascinato dentro il casolare. Io ho finto di essere svenuto, così ho orecchiato che tra loro si dicevano "Giulius sarà veramente soddisfatto di noi, ora". Dopo qualche ora i due malviventi si sono finalmente allontanati per andare a riferire credo, chiudendomi nella cascina sprovvista di telefono (ovviamente) e con le finestre blindate ermeticamente. Mi sono messo a frugare e ho trovato un cacciavite. E' stata la mia salvezza. Ho svitato i cardini della porta d'ingresso e sono venuto di corsa in commissariato". A quel punto il Srg. Panico fa entrare giulius che protesta e proclame la sua innocenza accusando a sua volta Nelson di aver inscenato una montatura per estrometterlo dalla società. Giulius replica al socio dicendo: "Impostore, ispettore lo interroghi per bene e vedrà che alla fine crollerà". L'ispettore allora esclama " Basta, così certo che interrogherò uno di voi due. L'altro può andare. Sergente Panico metta le manette a questo e lasci libero l'altro". Chi accusa l'ispettore Lumière? E perchè? (come qualcuno avrà notato i nomi di questo enigma sono tutti soprannomi apparteneti a un'unica persona, ma la storia per il resto è puramente casuale anche se un poco lunghetta) |
| ENIGMA 12 Luca L. 31 maggio 2004 [soluzioni] |
Qual è l'unico numero di 10 cifre
(scritto in base 10) con la seguente proprietà: la prima cifra (quella a sinistra) dice
quanti 0 ci sono nel numero, la seconda dice quanti 1 ci sono nel numero... la decima cifra dice quanti 9 ci sono nel numero. P.S. Si richiede di mostrare che tale numero è unico; dunque non è accettabile una risposta semplicemente del tipo: il numero è... |
| ENIGMA 11 Silvia P. 24 maggio 2004 [soluzioni] |
Un numero è formato da
dieci cifre, da 0 a 9 naturalmente, tutte diverse tra loro. Con queste stesse
cifre sono stati formati altri quattro numeri, che indichiamo con le lettere A, B, C
e D: A: 5 3 9 6 1 0 8 4 2 7 B: 3 6 1 7 9 4 8 0 5 2 C: 8 2 1 6 9 4 3 0 7 5 D: 9 2 1 8 5 0 3 7 4 6 Bisogna trovare il numero suddetto sapendo che: in A tre cifre sono nella stessa posizione rispetto al numero da trovare; in B e in D sono due le cifre nella stessa posizione del numero da trovare; in C sono due le cifre in posizione diversa rispetto al numero da trovare. |
| ENIGMA 10.2 Luca B. 17 maggio 2004 [soluzioni] |
Supponiamo di avere dei mattoncini tipo i lego
(base quadrata giusto per fissare le idee). Sfortunatamente abbiamo a disposizione solo
due tipi di mattoncini: i primi (in numero a piacere) di 8 cm d'altezza, gli altri (anche
questi in numero a piacere) di altezza 11 cm. Incastrandoli uno sopra l'altro si possono
formare "torri" di diverse altezze. La domanda è questa: quale è la misura della torre più alta fra quelle che non si possono in alcun modo costruire con i mattoni a disposizione? (naturalmente se quest'altezza esiste finita, se cioè non ci si trovi nel caso di altezze arbitrariamente grandi non raggiungibili esattamente). |
| ENIGMA 10.1 Luca B. 17 maggio 2004 [soluzioni] |
Ricavare una formula per esprimere la somma dei
primi n numeri interi. es: per n=3: 1+2+3; per n=5: 1+2+3+4+5 ecc... Naturalmente il bello non sta nella formula in sè (che probabilmente tutti conoscerete), ma nella sua dimostrazione -che può essere di qualsiasi tipo- per cercare di convincere anche chi è a digiuno di matematica della giustezza, appunto, di tale formula (...formula? manco si stesse parlando d'alchimia. avete migliori suggerimenti lessicali?) |
| ENIGMA 9 Giovanni V. 12 maggio 2004 [soluzioni] |
Trovare la successione di undici numeri interi
positivi, zero escluso, tra loro diversi, tali che la somma degli ultimi tre numeri sia
più piccola possibile. Ciò rispettando l'ulteriore condizione che la somma dei primi 3
deve essere minore della somma del 2°, 3° e 4°, che a sua volta deve essere minore di
quella del 3°, 4° e 5°, e così via fino agli ultimi 3. Spero di essere stato abbastanza chiaro. Le soluzioni possibili sono 2, il quesito, se volete cimentarvi direttamente, lo trovate anche qua, è il primo (era un'abbozzo di pagina di giochini matematici che avevo iniziato a preparare un po' di tempo fa, e ferma da allora): http://gve.altervista.org/quiz.html Già in tre me lo hanno chiesto, quindi chiedo scusa per l'imprecisione: i numeri necessari sono i soli numeri interi appartenenti nell'intervallo chiuso [1,11]. |
| ENIGMA 8 Elisa Elisa 3 maggio 2004 [soluzioni] |
Qual è quel numero che letto da destra a
sinistra è esattamente il doppio dello stesso numero letto da sinistra a destra? Mi sembra giusto dirvi che non si tratta dello zero. Si vuole un numero di 2 o più cifre... altrimenti sarebbe banale! |
| ENIGMA 7.2 Michela E. 26 aprile 2004 [soluzioni] |
[Prima di leggere questo enigma, conviene
leggere l'enigma 7.1, per capire meglio l'ambientazione, solitamente essenziale per la
risoluzione dei problemi!] Mentre i tre esploratori sono stati catturati e stanno subendo quello che vi ho raccontato finora, altri esploratori loro amici che erano un po' indietro rispetto a loro, sono riusciti a sfuggire alla cattura degli indiani e ora, nascosti dai massi e dai cactus stanno studiando un modo per penetrare nel campo e liberare i loro amici. Osservano il campo indiano: all'ingresso c'è una sentinella, il sagace Occhio Di Lince che ha il compito di far entrare solo quelli che rispondono correttamente alla sua parola d'ordine. Gli esploratori riescono ad avvicinarsi un po di più e sentono con maggiore precisione le parole scambiate dagli indiani. Prima di avvicina un indiano, Occhio Di Lince dice: DODICI e l'indiano risponde SEI! E Occhio Di Lince lo fa entrare. Poco dopo si avvicina un altro indiano, Occhio Di Lince dice OTTO e l'indiano risponde QUATTRO! E la sentinella lo fa entrare! Dopo cinque minuti si avvicina un terzo indiano, Occhio Di Lince dice SEI e l'indiano prontamente risponde TRE! E riesce ad entrare! A quel punto, un esploratore appena fresco della laurea di ingegneria (senza offesa :-P) si alza e dice ai compagni: -Ehi, ma questo un gioco da ragazzi!! Scusate, io mi sono fatto un mazzo così, ho passato al primo colpo e senza copiare Analisi 1 e Analisi 2 e so pure il principio di induzione!!! Questi giochetti primitivi mi fanno un baffo!!! E poi, scusate se è poco, io sono un ingegnere (anche col vecchio ordinamento!) Vado e tornerò vincitore. Mentre tutti approvano contenti che ci sia qualcuno che sappia districarsi in questa complicata situazione, l'esploratore-ingegnere si camuffa da indiano con un travestimento perfetto e poi si avvicina con incedere sicuro verso la sentinella. Occhio Di Lince dice: DUE e l'esploratore-ingegnere risponde sicuro: UNO! E ahimé, colpo di scena, viene catturato!!!! I compagni si domandano sbigottiti: perché? E sapendo che Occhio Di Lince non si era fumato una canna e che il travestimento dell'esploratore era realmente perfetto (tale da ingannare perfino il sagace Occhio Di Lince), qual era allora l'esatta risposta all'ultima parola d'ordine? |
| ENIGMA 7.1 Michela E. 26 aprile 2004 [soluzioni] |
Siamo nell'Arizona, con i suoi serpenti, cactus
e avvoltoi (in ogni vignetta di un fumetto che si rispetti tipo TEX (che non è il
programma usato dai matematici per compilare della matematica) nell'angolino in basso a
sinistra compare sempre un serpente che prende il sole su una pietra o un cactus o un
avvoltoio che attende la sua vittima). La tribù di Alce Tonante ha appena catturato tre
poveri esploratori che perlustravano la zona; i tre malcapitati sono stati legati al palo
della tortura e indiani inferociti si stanno dipingendo il viso con i colori della guerra
lanciando i loro tomhaws (si scrive cosi?) all'indirizzo delle teste dei tre impauriti
visi pallidi. All'improvviso dalla sua tenda il grande Alce Tonante in persona esce e si
rivolge ai prigionieri: -Augh! Grande capo Alce Tonante prende la parola! Oggi essere compleanno di Alce Tonante dunque grande capo indiano decide di dare una possibilità di salvezza ai tre visi pallidi. Alce Tonante ha in mano 5 cappelli, tre rossi e due neri, [anche il grande Alce Tonante era milanista e seguiva su SKY le partite] ora Alce Tonante prenderà 3 di questi cappelli e metterà un cappello in testa a ciascun viso pallido. Ogni viso pallido potrà vedere il colore del cappello degli altri due visi pallidi ma non il proprio (e ovviamente non quello degli altri due cappelli rimasti che Alce Tonante affiderà alla sua squaw Gazzella Che Corre). Chi riuscirà a indovinare il colore del proprio capello avrà salva la vita. Alce Tonante fa quello che aveva annunciato e poi comincia a interrogare i prigionieri. - Tu, viso pallido, di che colore hai il cappello? Il primo esploratore guarda il colore dei cappelli dei suoi due amici e afferma sconsolato: - Mi spiace, ma non sono in grado di determinarlo! Allora Alce Tonante si rivolge al secondo esploratore: - E tu, viso pallido, di che colore hai il cappello? Anche il secondo esploratore guarda il colore del cappello dei suoi due amici, ragiona su quello che ha detto il primo esploratore e infine esclama: - Mi spiace, anch'io non sono in grado di determinarlo! Alce Tonante allora tuona al suo popolo: - Bene, che i tre visi pallidi siano messi a morte!!! Mentre echeggiano le urla degli indiani che già bramano gli scalpi dei prigionieri il terzo esploratore che non era stato interrogato esclama con tutta la voce che ha in corpo: - Grande capo Alce Tonante!!!! Aspetta!!! In base a quello che posso vedere (cioè il colore dei cappelli dei miei due amici) e soprattutto ragionando su quello che hanno detto gli altri due esploratori, sono in grado di determinare con esattezza il colore del mio cappello! Di che colore è il cappello del terzo esploratore e qual è il ragionamento che ha fatto per determinarlo? |
| ENIGMA 6 Sergio R. 19 aprile 2004 [soluzioni] |
Abbiamo, incredibilmente, una
bella stanza chiusa lunga 30 piedi, larga 12 piedi e alta 12 piedi come da figura in
allegato: le pareti sono affrescate in stile minimalista e l'arredamento è un nichilista
antico. Sulla parete a destra, non so come sia entrata o chi l'abbia messa lì, troviamo
una formichina di nome Maicolsciumacher esattamente posta a un piede dal soffitto ed
equidistante dalle pareti laterali (quindi rispettivamente a 6 piedi da ogni parte). Sull'altra parete quadrata, quindi quella a sinistra per chi guarda il monitor, troviamo una goccia di miele dalle dimensioni che non ci interessano ed ovviamente non ci è dato sapere come ha fatto ad arrivar lì. La goccia è esattamente posta a un piede dal pavimento ed equidistante dalle pareti laterali (quindi rispettivamente a 6 piedi da ogni parte). Dando per scontato che: 1] la goccia non si muove; 1bis] riconoscendo la validità del diploma d'assaggiatore di miele del sig. Vertuan si specifica che non interessa il tipo di qualità di miele utilizzato; 2] la formica si muove a velocità costante, diversa da zero, solamente camminando (quindi senza salti, facendosi cadere o volando); 3] per la formica è indifferente camminare sul pavimento, le pareti verticali o il soffitto; 4] la stanza è chiusa come già sopraccitato ... ... quale è, se esiste, il percorso più breve in assoluto che la formichina deve fare per arrivare al miele?  |
| ENIGMA 5.2 Cesare T. 15 aprile 2004 [soluzioni] |
Due amici, A e B, ogni
riferimento a nomi di persone o cose realmente esistenti è puramente casuale e frutto di
(scarsa) fantasia, si incontrano dopo diversi anni e cominciano a conversare finché il
discorso va a finire sui figli. A : "Che età hanno i tuoi tre figli C,D ed E?" B : "Guarda, ti posso dire che il prodotto delle loro età è uguale a 36". A : "Oh, pero`... questa si` che e` una risposta sbrigativa. Comunque questa informazione purtroppo non mi basta !" B : "È vero; ti dirò allora che la somma delle loro tre età è uguale al numero civico di quella casa". A : "Uhm... (pensando tra se e se: questo è proprio matto); però ancora non mi hai risposto." B : "Hai ragione. Ti posso dire che il più piccolo ha gli occhi azzurri!" A : Oh, perdindirindina è tardissimo! Scusa, ma devo andare, sai devo dar da mangiare alla sfinge. Veniamo dunque al quesito. L'amico A ha mollato la conversazione perché B era visibilmente squilibrato e voleva divincolarsi, ma non si é accorto che B gli ha dato tutti gli elementi per estrarre l'età dei suoi figli. Qual è l'età dei tre figli? |
ENIGMA 5.1 |
Il problema è quasi impossibile
da porre scrivendo, ma io ci proverò lo stesso... se sarò chiaro bene, se no mi scuso. Sia dato un cubo (che chiamerò cubone) simile al cubo di Rubik fatto di 27(=3*3*3) cubi piu` piccoli (d'ora in poi cubetti) affiancati ed incollati in modo che ce ne stiano tre per spigolo del cubone. Voglio tagliare il cubone nei suoi cubetti. Un modo sarebbe tagliare il cubo in tre parti lungo la direzione perpendicolare ad x con 2 tagli. Poi altri due tagli nella direzione perpendicolare a y ancora equidistanziati cosicché il cubone visto dalla direzione z apparirà diviso in 9 quadratini (parallelepipedi formati da tre cubetti): O|O|O -+-+- O|O|O -+-+- O|O|O Con gli ultimi 2 tagli nella direzione perpendicolare a z si conclude poi il lavoro. Un totale di 6 tagli. Ora aggiungo una possibilità: spostare le regioni tagliate prima del taglio successivo. Ad esempio dopo un primo taglio OO|O OO|O OO|O potrei fare una mossa che mi porti alla configurzione OOO --- OO OO OO e fare un secondo taglio O|OO -+-- O|O O|O O|O Dopo il secondo taglio il cubone è maggiormente frazionato dato che ho tagliato 4*3 legami anziche` 3*3. Continuando così si potrebbe pensare che è possibile separare il cubone con meno di 6 mosse... invece no! Per questo c'è una dimostrazione elegantissima che vi chiedo di trovare. |
| ENIGMA 4.2 Sofia S. 29 marzo 2004 [soluzioni] |
Sulle 64 caselle di una classica
scacchiera si dispongano i numeri naturali da 1 a 64. Chiamiamo SORELLE due caselle che
hanno un lato in comune (per stare nelle notazioni di Anita, sono sorelle due caselle
sulle quali riesco a sovrapporre un pezzo di domino). È possibile disporre i numeri
sulla scacchiera in modo che la differenza tra i numeri presenti su due caselle SORELLE
sia sempre al massimo 4? Se è possibile, si chiede di mostrare (almeno) una disposizione coerente con le richieste. Eventualmente, si chiede di classificare tutte le possibili disposizioni. Se non fosse possibile, si chiede di dimostrare il perché. In questo caso, tutti i sistemi sono possibili. Ma vi prego... evitiamo l'elencazione di tutte le disposizioni possibili...! A proposito, quante sarebbero? |
| ENIGMA 4.1 Sofia S. 29 marzo 2004 [soluzioni] |
Come "dimostrereste" il teorema di Pitagora (equivalenza tra il quadrato costruito sull'ipotenusa e la somma dei due quadrati costruiti sui cateti di un triangolo rettangolo) alla solita persona (vedi il primo enigma proposto da Paolo) che non sa nulla di geometria? |
| ENIGMA 3 Anita P. 22 marzo 2004 [soluzioni] |
Avete la classica scacchiera 8x8 e 31 pezzi di
domini ognuno dei quali copre due caselle adiacenti della scacchiera. È possibile disporre i pezzi di domino sulla scacchiera in modo da lasciar scoperte le due estremità di una delle due diagonali principali? |
| ENIGMA 2 Davide B. 22 marzo 2004 [soluzioni] |
Ne ho quattro, ne taglio uno, ne cadono tre e ne
rimangono cinque. Che cosa sono? |
ENIGMA 1.2 |
Ci troviamo in asia minore, verso la fine del
XXI secolo, in un convento di monaci... non vi dico il nome tanto non li conoscete. Questi
monaci fanno voto di silenzio. Vale a dire che non comunicano tra di loro, in nessun modo,
ne per iscritto, ne si parlano e nemmeno comunicano con gesti o sguardi. I monaci nel
convento sono 24. Si incontrano una sola volta al giorno, per pregare, ogni mattina in
coro.La notte di natale dell'anno 1056 ogni monaco riceve la seguente comunicazione da
parte del vescovo: "Cari monaci, sappiamo con certezza che una terribile epidemia è entrata nel vostro monastero. Non sappiamo dirvi quanti di voi sono affetti da questa malattia, ma sappiamo che almeno uno di voi lo è. La malattia non è contagiosa, non guarisce da sola (1) e ha come unico sintomo la comparsa, nel mezzo della fronte di una vistosa macchia rossa. È necessario che ognuno di voi esca immediatamente dal convento per ricevere le cure necessarie, appena ha la certezza di essere malato (2)". Nel monastero naturalmente non ci sono specchi (ne ci si può specchiare in pozzanghere o fontane) e come detto i monaci non possono comunicare. L'unico incontro è quello della preghiera cominitarioa mattutina nel quale ogni monaco vede tutti gli altri, e può decidere se uscire oppure no. La mattina seguente (mattina 25 dicembre) i monaci si incontrano per la preghiera e al termine della preghiere nessun monaco esce dal convento per farsi curare. Anche la mattina seguente accade la stessa cosa, i monaci si incontrano ma nessuno di essi esce. E così accade tutte le altre mattine. Fino alla mattina del 1 gennaio 1056 (mattina dell'ottavo giorno dopo l'annuncio del vescovo) in cui, dopo la preghiera, TUTTI E SOLI i monaci malati escono insieme dal convento per ricevere le cure. La domanda è: QUANTI SONO I MONACI CHE ESCONO DAL CONVENTO? IPOTESI AGGIUNTIVE: Chiaramente si assuma come ipotesi l'assoluta onestà dei monaci e la loro assoluta abilità in logica. Si assuma anche come ipotesi che tutti i monaci si presentano sempre per la preghiera del mattino, a meno che non siano usciti dal convento per le cure. NOTE: (1) Se un monaco è malato la notte del 25, rimane sempre malato, se non è malato, rimane sempre sano. (2) Se un monaco esce dal convento i monaci se ne accorgono il giorno seguente, non vedendolo alla preghiera. |
ENIGMA 1.1 |
Avete tra le mani un foglio bianco di carta. Il
foglio è quadrato e il lato misura 12 cm. Naturalmente l'area del foglio misura 144 cm2.
Da questo foglio ne volete ottenere un'altro la cui area sia la metà: 72 cm2.
Purtroppo avete pochissimo tempo, e non avete ne righello ne forbici. Come fate? Supponete ora di trovarvi di fronte una persona che non sa nulla di matematica e di geometria (non sa cosa è una radice quadrata, non conosce il teorema di Pitagora and così via) e di doverla convincerla che cio che avete fatto è giusto, cioè che avete ottenuto un quadrato di area pari alla metà del quadrato originale. Come fate? |
ENIGMA 0.2 |
Un soldato deve fare esplodere un ponte. In
particolare i suoi ordini sono di farlo saltare di lì a 45 minuti. Il problema è che il
soldato non ha nessuno strumento che gli consenta di misurare il tempo, fatta eccezione
per due micce che gli sono avanzate dopo aver minato il ponte e che durano esattamente 1
ora ciascuna. Purtroppo le micce non bruciano in modo regolare (tipo non è che dopo
mezz'ora è bruciata metà di una miccia o dopo 20 minuti un terzo: la velocità con cui ogni miccia brucia cambia nel corso della combustione, solo il tempo totale impiegato dalla miccia a bruciare completamente è sempre 1 ora). Come fare per far detonare il ponte nel momento corretto? |
ENIGMA 0.1 |
Su un tavolo sono disposte in due file sei
carte, ciascuna con stampato un numero di una cifra, in questo modo: 3 4 5 6 7 8 Spostandone due e solo due, è possibile fare in modo che la somma delle cifre della prima fila sia uguale alla somma delle cifre della seconda. Come fare? |
